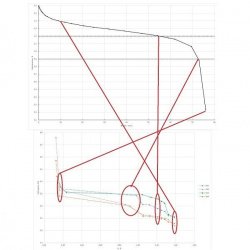
Изменение импеданса (1 кГц) LR44 в процессе разряда. Про внутреннее сопротивление и способы его измерения
Это как бы дополнение к предыдущим статьям. Сначала хотел написать краткий отчет по LR44 Epilso. Но в первой части кратко высказать ряд соображений. «И тут Остапа понесло», коротко не получилось.
В принципе, многословную первую часть можно и пропустить. Но тогда не будет понятна суть «Заключения».
Измерение т.н. внутреннего сопротивления химических источников тока (ХИТ) — сокровенная мечта всех, кто хоть как-то связан с батарейками и аккумуляторами.
Одно плохо — сделать корректный замер внутреннего сопротивления ХИТ нельзя. Потому что это не есть некая постоянная, а функция, в общем случае зависящая от:
— уровня заряда ХИТ
— температуры
— уровня нагрузки (силы тока, протекающего в замкнутой цепи)
— способа и методики измерения.
И если первые два параметра еще хоть как-то можно зафиксировать (полный заряд, комнатная температура), то третий и четвертый моменты полностью противоречат самому понятию «омическое сопротивление» как некой константе.
Отмазка.
Много лет собирался и наконец решился опубликовать данный материал. Я попытался изложить все максимально понятно, поэтому начинаю с общеизвестного и вроде как даже очевидного. Но, чем дальше в лес, тем громче песня (старинная зулусская мудрость). Может, кому-то будет интересно.
В конечном итоге: все, что написано в данной главе — это ИМХО, а не истина в последней инстанции.
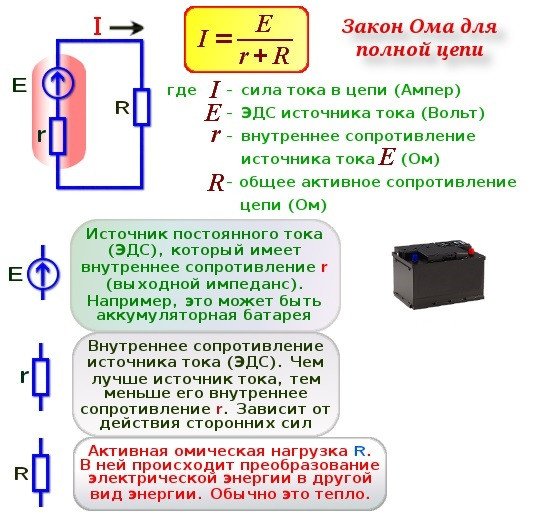
1) Есть такой замечательный закон Ома для полной цепи. Скорее всего, Георг Симон Ом не имеет к нему прямого отношения (ИМХО) — это «творческое обобщение» закона Ома для замкнутой цепи, где в качестве источника электричества выступает некий гальванический элемент или батарея из оных. Картинка из интернетов:
 Тут сразу 2 вопроса:
Тут сразу 2 вопроса:
1) что произойдёт, если величину нагрузочного сопротивления R изменить?
2) как экспериментально измерить величину того самого «внутреннего сопротивления r»?
Отвечаю:
1) изменится r.
2) да легко, но r зависит от кучи факторов (см. выше) и всегда будут получаться разные r.
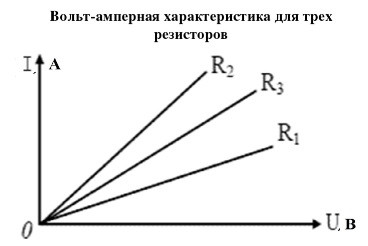
2) Почему для резистора, куска провода и подобных «линейных» объектов имеет смысл использовать некую величину R=U/I=const? Потому что в относительно широких диапазонах напряжения и силы тока у них ВАХ линейная
 А вот как выглядит ВАХ простого и незамысловатого выпрямляющего диода
А вот как выглядит ВАХ простого и незамысловатого выпрямляющего диода
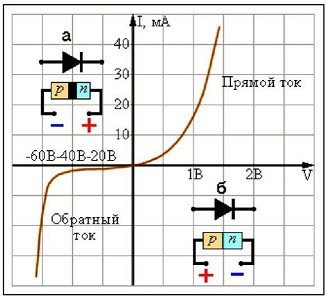 Скажите, чему равно «внутреннее сопротивление» устройства с такой ВАХ и в чем его тайный физический смысл?
Скажите, чему равно «внутреннее сопротивление» устройства с такой ВАХ и в чем его тайный физический смысл?
Самое печальное, что любой ХИТ устроен значительно сложнее любого самого разнеможного диода. А принципы накопления и отдачи заряда в оном на порядки сложнее, чем в любом конденсаторы, включая ионисторы. Ибо внутри ХИТ происходит двойное преобразование энергии: при заряде электрическая энергия превращается в энергию химических связей, а при разряде — все наоборот. Плюс возможное протекание побочных процессов. Плюс процессы в ДЭС (переходных слоях между электролитом и активными массами катода и анода). Возможно, еще что-то забыл. Но не суть — итак понятно, что дело это темное.
3) Как говорится, если нельзя, но очень хочется, то можно. Наверное, именно так рассуждали джентльмены из МЭК.
И поэтому в своих замечательных рекомендациях (которые потом практически неминуемо становятся ГОСТами различных стран) они-таки предложили делать замеры «внутреннего сопротивления» ХИТ. Причем аж 2-мя способами: на постоянном токе R(d.c.) и переменном токе R(a.c.).
4) Замеры R(d.c.) и почему это прикольно
Если совсем кратко, то для наиболее распространенных ЭХ систем МЭК рекомендует использовать вот такое
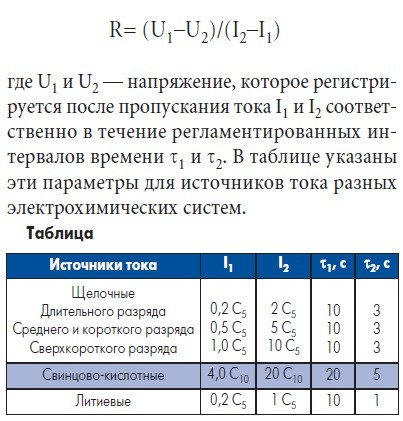 Что бы оценить насколько логичны подобные рекомендации предлагаю провести небольшое расследование. Возьмём первую строчку из таблички и посмотрим что получится в случае общеизвестных «белых» Энелупов ААА. Для начала, нам нужно получить экспериментальные кривые разряда в широком диапазоне нагрузок.
Что бы оценить насколько логичны подобные рекомендации предлагаю провести небольшое расследование. Возьмём первую строчку из таблички и посмотрим что получится в случае общеизвестных «белых» Энелупов ААА. Для начала, нам нужно получить экспериментальные кривые разряда в широком диапазоне нагрузок.
 Ибо все было получено до нас и представлено в даташите BK-4MCC.
Ибо все было получено до нас и представлено в даташите BK-4MCC.
 Далее в любом граф. редакторе наложим мелкую сетку (для более удобного определения координат точек) и сделаем разрезы при разных значениях отданной емкости: от 100 до 600 мАч. R находится как (U₁-U₂)/(I₂-I₁). U₁ и I₁ во всех случаях — для тока разряда 0.2С (160 мА).
Далее в любом граф. редакторе наложим мелкую сетку (для более удобного определения координат точек) и сделаем разрезы при разных значениях отданной емкости: от 100 до 600 мАч. R находится как (U₁-U₂)/(I₂-I₁). U₁ и I₁ во всех случаях — для тока разряда 0.2С (160 мА).
 На картинке это выглядит вот так
На картинке это выглядит вот так
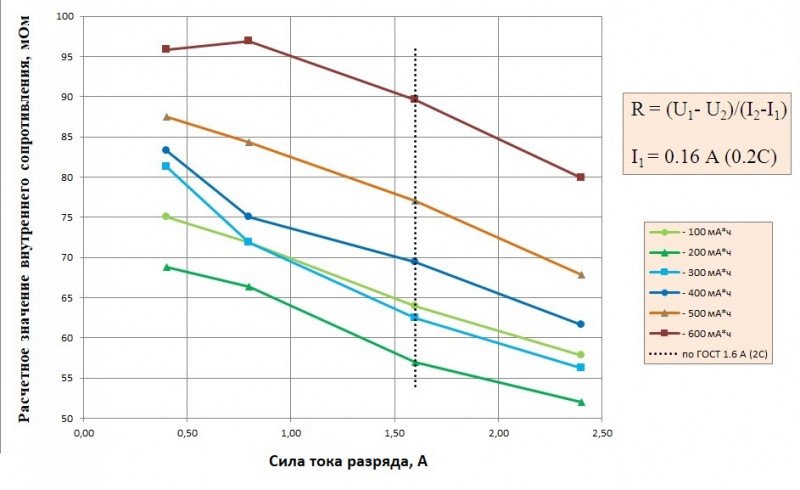 А здесь показано как все изменяется в процессе разряда:
А здесь показано как все изменяется в процессе разряда:
 Особенно пикантно выглядит провал при 200 мАч.
Особенно пикантно выглядит провал при 200 мАч.
Но главный прикол в другом: разрядные токи 0.2С и 2.0С — ничем не примечательны. Могли быть выбраны («рекомендованы») любые другие пары токов разряда. Даже если зафиксировать I₁ = 0.2С = 160 мА и поварьировать I₂ в промежутке 0.5С...3.0С, то можно получить любые R(d.c.) в промежутке 52...97 мОм. Это для различных значений отданной емкости 100...600 мАч. Конечно, ежели этот параметр зафиксировать, то разбежка будет не в 2 раза, а несколько меньше. Но тоже достаточно заметная. Рекордный разброс наблюдается при 300 мАч: 56...81 мОм. В 1.45 раза.
Почему же так получается?
Формальное объяснение: R(d.c.) часто представляют как сумму двух сопротивлений: «омического» и «поляризационного» R(d.c.) = R(о) + R(p).
 Считается, что R(о) зависит только от температуры и при T=const:
Считается, что R(о) зависит только от температуры и при T=const:
— практически не зависит от величины нагрузки
— почти не меняется до снятия 70-90% полной емкости ХИТ.
Для R(p) — все наоборот. Чем больше нагрузка и чем сильнее разряжена ячейка, тем больше R(p). Такое поведение R(p) является первопричиной проблем с измерением R(d.c.). Какие элементы конструкции ХИТ определяют R(о) и R(p) — будет показано в следующем пункте.
5) Измерения R(a.c.) на фиксированной частоте 1 кГц — типа, «правильные» и «наше все»
Вообще-то, в англоязычном варианте R(a.c.) есть ни что иное как «Internal Impedance» (внутренний импеданс).
В ГОСТ-Р-МЭК-61557-1-2005 сделан достаточно аккуратный перевод на русский:
 Обратите внимание: «импеданс» vs «сопротивление» и даже буковками обозначено разными (Z vs R). Наверное, что бы не путали теплое с мягким.
Обратите внимание: «импеданс» vs «сопротивление» и даже буковками обозначено разными (Z vs R). Наверное, что бы не путали теплое с мягким.
А вот в русскоязычных ГОСТах на аккумуляторы и батарейки — все по-простому. Есть некое «внутреннее сопротивление» ХИТ и меряют его 2 способами: на постоянном токе R(d.c.) или на переменном токе R(a.c.). Причем, «импеданс приблизительно равен сопротивлению».
ГОСТ Р МЭК 61960-3-2019 (ранее — ГОСТ Р МЭК 61960-2007):
 Какому-такому «сопротивлению»? Или R(a.c.)≈R(d.c.) [если я правильно понял тайный смысл примечания от составителей родного ГОСТа].
Какому-такому «сопротивлению»? Или R(a.c.)≈R(d.c.) [если я правильно понял тайный смысл примечания от составителей родного ГОСТа].
Давайте посмотрим, насколько R(a.c.) «примерно равно» R(d.c.).
Берем 2 корейских даташита на литий-ион 18650.
Первый — Samsung INR18650-25R. Оказывается, 13 мОм ≈ 22 мОм. Так и запишем…
 Второй — LG 18650HE4, в миру — «банан» из-за специфической расцветки. Здесь 14 мОм ≈ 24 мОм. Прелестно.
Второй — LG 18650HE4, в миру — «банан» из-за специфической расцветки. Здесь 14 мОм ≈ 24 мОм. Прелестно.
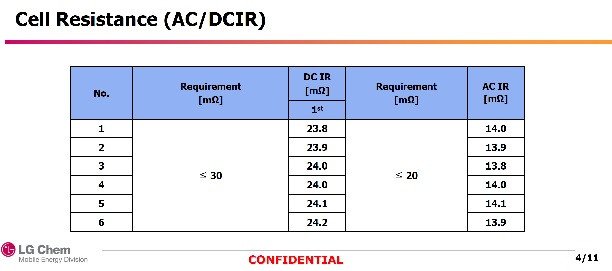 Ну и ладно. В конечном итоге, уже разобрались, что измерения R(d.c.) — это неблагодарное занятие. А вот мерять R(a.c.) на фиксированной частоте 1 кГц — «и хорошо, и правильно, и куда точнее измерений R(d.c.)». [Кто автор этой сентенции — мне не ведомо.].
Ну и ладно. В конечном итоге, уже разобрались, что измерения R(d.c.) — это неблагодарное занятие. А вот мерять R(a.c.) на фиксированной частоте 1 кГц — «и хорошо, и правильно, и куда точнее измерений R(d.c.)». [Кто автор этой сентенции — мне не ведомо.].
Давайте разберёмся, что есть измерение импеданса на фиксированной частоте (1 кГц или иной) и какую полезную информацию оно несет о богатом внутреннем мире ХИТ вообще и о внутреннем сопротивлении в частности.
На самом деле, на ресурсе давно как присутствует статья по этому поводу. Но она слишком большая, слишком подробная и давно забыта.
Надеюсь, что такое импеданс читателю известно. В нулевом приближении эквивалентная схема [замещения] любого ХИТ может быть представлена следующим образом:
 На самом деле, полные эквивалентные схемы реальных аккумуляторов и батареек несколько сложнее. К примеру, для литий-ионного аккумулятора что-то типа такого:
На самом деле, полные эквивалентные схемы реальных аккумуляторов и батареек несколько сложнее. К примеру, для литий-ионного аккумулятора что-то типа такого:
 Что такое W (элементы Варбурга) и почему в трех случаях емкости были заменены на CPE (элементы постоянной фазы) — желающие могут глянуть в той самой большой статье.
Что такое W (элементы Варбурга) и почему в трех случаях емкости были заменены на CPE (элементы постоянной фазы) — желающие могут глянуть в той самой большой статье.
Но на самом деле, все эти ужасы нам не нужны. Для дальнейшего изложения вполне подойдет эквивалентная схема чуть сложнее первой.
Давайте представим (в порядке бреда), что у нас есть приборчик а-ля Hioki CHEMICAL IMPEDANCE ANALYZER IM3590.
 Это тоже измеритель импеданса, типа всенародно-доступных YR1030/1035/1035+ и подобных. Но есть несколько небольших [шутка юмора] отличия:
Это тоже измеритель импеданса, типа всенародно-доступных YR1030/1035/1035+ и подобных. Но есть несколько небольших [шутка юмора] отличия:
— IM3590 меряет импеданс ХИТ не на строго определённой частоте (1 кГц), а в широком интервале (1 mHz to 200 kHz), т.е. снимает спектр
— для анализа позволяет использовать эквивалентные схемы
— стоит как крыло от самолета.
Вот, к примеру, берем какой-нибудь литий-ионный аккумулятор (из статьи в журнале «Электрохимия», 2009, №1, с. 42-48) и смотрим этот самый импедансный спектр. В данном случае он представлен как годограф в координатах Найквиста, но не суть. С большой вероятностью стрелки указывают не на конкретные точки 1 кГц, 100Гц и т.д., а на области порядков частот.
 Делаем его «расшифровку» (подробно — в той самой большой статье). И получаем примерно такое.
Делаем его «расшифровку» (подробно — в той самой большой статье). И получаем примерно такое.

 Наибольший интерес представляют 2 точки:
Наибольший интерес представляют 2 точки:
1) Пересечение годографа с осью «Х». R(о) = 33 мОм
2) Пересечение второй окружности с осью «Х». R(d.c.) = R(о)+R(p) = 47 мОм
Некоторые замечания.
► Если повезет, и пересечение годографа с осью «Х» случится при 1 кГц (или сильно рядом), то поздравляю — Вы теперь знаете R(о). Одно плохо — это всего лишь часть активного сопротивления ХИТ.
► Как узнать повезло или не повезло? Да никак. Стрельба по мишени с завязанными глазами.





► Еще один момент. В импедансометрах используется синусоидальное напряжение с малым размахом: единицы-десятки мВ. В результате — синусоида тока имеет размах не более десятков мА.
 Смысл столь малых нагрузок — исследование системы в состоянии, близком к равновесному. Поэтому измеренные значения R(о) = 33 мОм, R(p) = 47-33 = 14 мОм и общее активное сопротивление R(о)+R(p) = 47 мОм соответствуют сверхмалой нагрузке на ячейку. Что же произойдет, если через ячейку будут протекать токи в сотни мА или еще больше? R(о) — практически не изменится, на то оно и «омическое»;). А R(p) увеличится. Соответственно увеличится и активное сопротивление (см. выше пример с Энелупом). Причем, R(a.c.,1kHz) — это всего лишь некоторая часть R(о)+R(p). В общем случае неизвестная. Если не заморачиваться с дополнительными замерами. А если заморачиваться, то R(a.c.,1kHz) становится не нужным.
Смысл столь малых нагрузок — исследование системы в состоянии, близком к равновесному. Поэтому измеренные значения R(о) = 33 мОм, R(p) = 47-33 = 14 мОм и общее активное сопротивление R(о)+R(p) = 47 мОм соответствуют сверхмалой нагрузке на ячейку. Что же произойдет, если через ячейку будут протекать токи в сотни мА или еще больше? R(о) — практически не изменится, на то оно и «омическое»;). А R(p) увеличится. Соответственно увеличится и активное сопротивление (см. выше пример с Энелупом). Причем, R(a.c.,1kHz) — это всего лишь некоторая часть R(о)+R(p). В общем случае неизвестная. Если не заморачиваться с дополнительными замерами. А если заморачиваться, то R(a.c.,1kHz) становится не нужным.

► Второй интересный момент. Есть мнение что для «обычных» литий-ионных аккумуляторов условие R(о)≈R(a.c.,1kHz) нередко соблюдается. Для Li/LiFePO₄ — вроде как нет. Та же самая Hioki на голубом глазу заявляет: «Этот сигнал переменного тока обычно имеет фиксированную частоту 1 кГц...» и приводит идеализированную картинку (правда, забывает уточнить, что такое бывает в случае литий-иона, да и то не всегда)
 А вот продолжение: "… хотя некоторые продукты позволяют изменять частоту. В последнее время все больше и больше производителей предпочитают проводить испытания внутреннего сопротивления на нескольких частотах, чтобы более эффективно обнаруживать дефектные элементы."
А вот продолжение: "… хотя некоторые продукты позволяют изменять частоту. В последнее время все больше и больше производителей предпочитают проводить испытания внутреннего сопротивления на нескольких частотах, чтобы более эффективно обнаруживать дефектные элементы."
Суть в том, что Hioki производит импедансометры как для фиксированной частоты 1 кГц, так и позволяющие снимать спектр. А продавать надо и то и другое.;)
► И еще один интересный момент. В ходе горячего обсуждения очередного «измерителя внутреннего сопротивления аккумуляторов» на 1 кГц был пост ув. virus_59, в коем меня заинтересовал один момент:
Поэтому правило «чем меньше импеданс R(a.c.,1kHz) — тем больше высокотоковость» в ряде случаев может и не выполняться. Даже для литий-иона. Про остальные ЭХ системы вообще молчу. А кто сказал, что будет легко? :)
6) Имеет ли смысл измерять R(a.c.,1kHz)?
Конечно имеет. Ибо на безрыбье и рак… сами понимаете. Только учитывать некоторые моменты, изложенные выше. Применительно к данной статье: R(a.c.) LR44, измеренное посредством YR1035, безусловно будет отличаться от активного сопротивления R(о)+R(p). Но вряд ли будет отличаться больше чем на порядок. Это с запасом.
После предыдущих измерений (часть1, часть2) осталось 4 штуки LR44 Epilso.
 Они были помещены в держатели с припаянными резисторами ~ 680 Ом и подвергнуты дробному разряду.
Они были помещены в держатели с припаянными резисторами ~ 680 Ом и подвергнуты дробному разряду.
 Суть в следующем:
Суть в следующем:
— батарейки разряжались некоторое время (от 4 до 12 ч.)
— затем изменялось напряжение на клеммах под нагрузкой
— потом батарейки вынимались из держателей, производились замеры импеданса и разности потенциалов без нагрузки. Но не сразу, а по истечении 30-60 мин., когда все более-менее устаканится (деполяризация ячейки).
Но смысл данной статьи — не в разрядных кривых.
А в том, что же происходит с импедансом ячеек LR44 в процессе их разряда?
Насколько заметно он увеличивается на различных стадиях разряда?
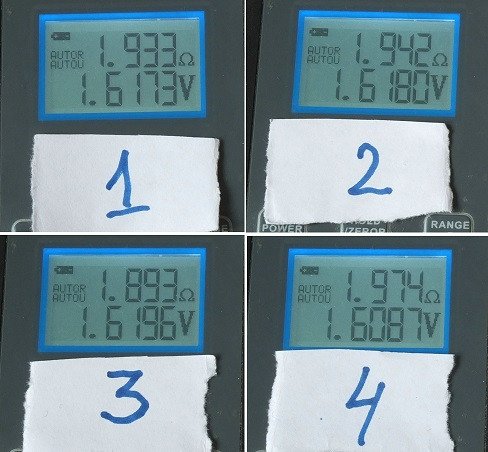
НРЦ (напряжение разорванной цепи) и импедансы ячеек весьма единообразны.
Если совсем кратко, то как-то так:
 Пунктирные линии — для U под нагрузкой. Сплошные — НРЦ после «отдыха» 30-60 мин, когда импеданс более-менее стабилизируется. Разница только в координатах экспериментальных точек по оси абсцисс.
Пунктирные линии — для U под нагрузкой. Сплошные — НРЦ после «отдыха» 30-60 мин, когда импеданс более-менее стабилизируется. Разница только в координатах экспериментальных точек по оси абсцисс.
Более подробно — под спойлером.
Еще один вариант представления: какие значения импеданса примерно соответствуют участкам на разрядной кривой. Может, кому-то так будет более понятно.
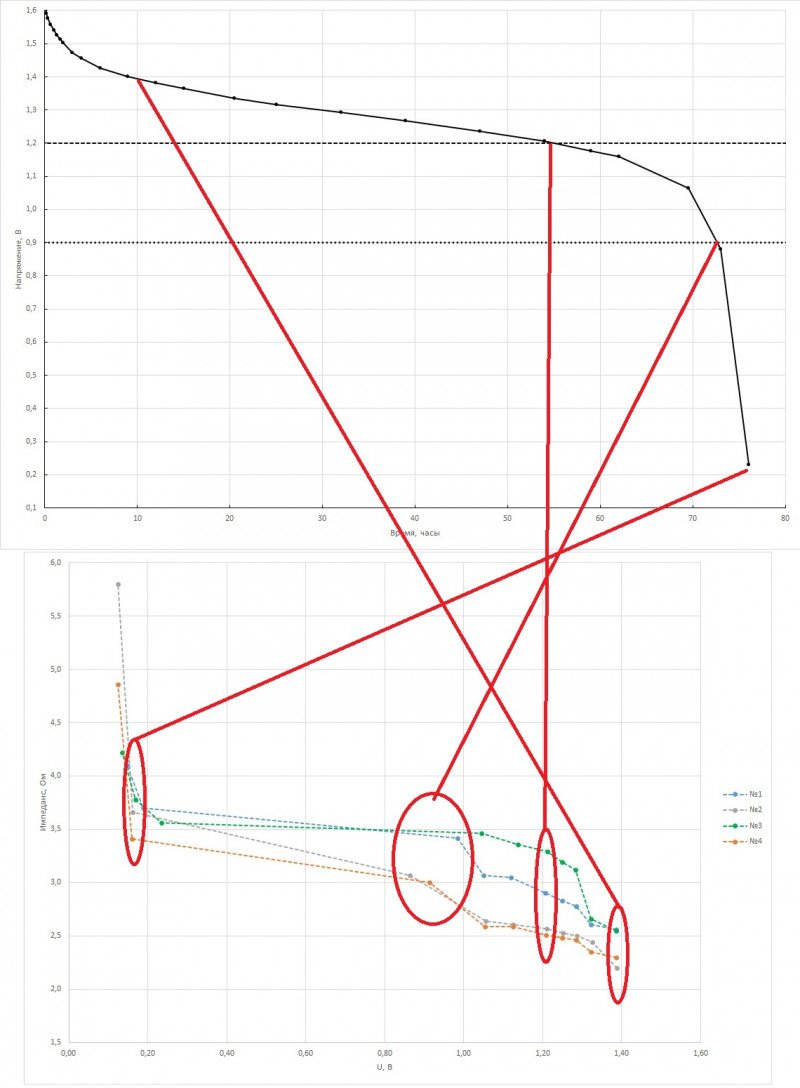
Судя покрайней последней картинке, импеданс на 1 кГц всегда меньше 3.5 Ω вплоть до 0.9 В (под нагрузкой).
Если предположить, что измеряемые значения импеданса LR44 Epilso отличаются от т.н. «внутреннего сопротивления» не более чем на порядок, то в расчётах емкости
Емкость = I·t = (U/R)·t
величиной r можно пренебречь. R = Rн + r ≈ Rн, Rн — сопротивление нагрузочного резистора. А емкость батареек на отсечках 1.2В и 0.9В при Rн = 680 Ω ТУТ и ТУТ определена достаточно корректно.
P.S. Когда материал был уже готов к публикации, я таки придумал как экспериментально оценить насколько сильно импеданс (1 кГц) LR44 отличается от общего активного сопротивления при Rн=680 Ω. Может, всего в 1.5-2 раза, а не на целый порядок? Оказалось, что мой пессимизм был обоснован. Или я что-то делал не так. Подробности под спойлером.
И на этом все. Всего доброго.
В принципе, многословную первую часть можно и пропустить. Но тогда не будет понятна суть «Заключения».
Преамбула. Про «внутреннее сопротивление» ХИТ и способы его измерения
Измерение т.н. внутреннего сопротивления химических источников тока (ХИТ) — сокровенная мечта всех, кто хоть как-то связан с батарейками и аккумуляторами.
Одно плохо — сделать корректный замер внутреннего сопротивления ХИТ нельзя. Потому что это не есть некая постоянная, а функция, в общем случае зависящая от:
— уровня заряда ХИТ
— температуры
— уровня нагрузки (силы тока, протекающего в замкнутой цепи)
— способа и методики измерения.
И если первые два параметра еще хоть как-то можно зафиксировать (полный заряд, комнатная температура), то третий и четвертый моменты полностью противоречат самому понятию «омическое сопротивление» как некой константе.
Отмазка.
Много лет собирался и наконец решился опубликовать данный материал. Я попытался изложить все максимально понятно, поэтому начинаю с общеизвестного и вроде как даже очевидного. Но, чем дальше в лес, тем громче песня (старинная зулусская мудрость). Может, кому-то будет интересно.
В конечном итоге: все, что написано в данной главе — это ИМХО, а не истина в последней инстанции.
1) Есть такой замечательный закон Ома для полной цепи. Скорее всего, Георг Симон Ом не имеет к нему прямого отношения (ИМХО) — это «творческое обобщение» закона Ома для замкнутой цепи, где в качестве источника электричества выступает некий гальванический элемент или батарея из оных. Картинка из интернетов:
 Тут сразу 2 вопроса:
Тут сразу 2 вопроса:1) что произойдёт, если величину нагрузочного сопротивления R изменить?
2) как экспериментально измерить величину того самого «внутреннего сопротивления r»?
Отвечаю:
1) изменится r.
2) да легко, но r зависит от кучи факторов (см. выше) и всегда будут получаться разные r.
2) Почему для резистора, куска провода и подобных «линейных» объектов имеет смысл использовать некую величину R=U/I=const? Потому что в относительно широких диапазонах напряжения и силы тока у них ВАХ линейная
 А вот как выглядит ВАХ простого и незамысловатого выпрямляющего диода
А вот как выглядит ВАХ простого и незамысловатого выпрямляющего диода Скажите, чему равно «внутреннее сопротивление» устройства с такой ВАХ и в чем его тайный физический смысл?
Скажите, чему равно «внутреннее сопротивление» устройства с такой ВАХ и в чем его тайный физический смысл? Самое печальное, что любой ХИТ устроен значительно сложнее любого самого разнеможного диода. А принципы накопления и отдачи заряда в оном на порядки сложнее, чем в любом конденсаторы, включая ионисторы. Ибо внутри ХИТ происходит двойное преобразование энергии: при заряде электрическая энергия превращается в энергию химических связей, а при разряде — все наоборот. Плюс возможное протекание побочных процессов. Плюс процессы в ДЭС (переходных слоях между электролитом и активными массами катода и анода). Возможно, еще что-то забыл. Но не суть — итак понятно, что дело это темное.
3) Как говорится, если нельзя, но очень хочется, то можно. Наверное, именно так рассуждали джентльмены из МЭК.
И поэтому в своих замечательных рекомендациях (которые потом практически неминуемо становятся ГОСТами различных стран) они-таки предложили делать замеры «внутреннего сопротивления» ХИТ. Причем аж 2-мя способами: на постоянном токе R(d.c.) и переменном токе R(a.c.).
4) Замеры R(d.c.) и почему это прикольно
Если совсем кратко, то для наиболее распространенных ЭХ систем МЭК рекомендует использовать вот такое
 Что бы оценить насколько логичны подобные рекомендации предлагаю провести небольшое расследование. Возьмём первую строчку из таблички и посмотрим что получится в случае общеизвестных «белых» Энелупов ААА. Для начала, нам нужно получить экспериментальные кривые разряда в широком диапазоне нагрузок.
Что бы оценить насколько логичны подобные рекомендации предлагаю провести небольшое расследование. Возьмём первую строчку из таблички и посмотрим что получится в случае общеизвестных «белых» Энелупов ААА. Для начала, нам нужно получить экспериментальные кривые разряда в широком диапазоне нагрузок. Ибо все было получено до нас и представлено в даташите BK-4MCC.
Ибо все было получено до нас и представлено в даташите BK-4MCC. Далее в любом граф. редакторе наложим мелкую сетку (для более удобного определения координат точек) и сделаем разрезы при разных значениях отданной емкости: от 100 до 600 мАч. R находится как (U₁-U₂)/(I₂-I₁). U₁ и I₁ во всех случаях — для тока разряда 0.2С (160 мА).
Далее в любом граф. редакторе наложим мелкую сетку (для более удобного определения координат точек) и сделаем разрезы при разных значениях отданной емкости: от 100 до 600 мАч. R находится как (U₁-U₂)/(I₂-I₁). U₁ и I₁ во всех случаях — для тока разряда 0.2С (160 мА). На картинке это выглядит вот так
На картинке это выглядит вот так А здесь показано как все изменяется в процессе разряда:
А здесь показано как все изменяется в процессе разряда: Особенно пикантно выглядит провал при 200 мАч.
Особенно пикантно выглядит провал при 200 мАч.Но главный прикол в другом: разрядные токи 0.2С и 2.0С — ничем не примечательны. Могли быть выбраны («рекомендованы») любые другие пары токов разряда. Даже если зафиксировать I₁ = 0.2С = 160 мА и поварьировать I₂ в промежутке 0.5С...3.0С, то можно получить любые R(d.c.) в промежутке 52...97 мОм. Это для различных значений отданной емкости 100...600 мАч. Конечно, ежели этот параметр зафиксировать, то разбежка будет не в 2 раза, а несколько меньше. Но тоже достаточно заметная. Рекордный разброс наблюдается при 300 мАч: 56...81 мОм. В 1.45 раза.
Почему же так получается?
Формальное объяснение: R(d.c.) часто представляют как сумму двух сопротивлений: «омического» и «поляризационного» R(d.c.) = R(о) + R(p).
 Считается, что R(о) зависит только от температуры и при T=const:
Считается, что R(о) зависит только от температуры и при T=const:— практически не зависит от величины нагрузки
— почти не меняется до снятия 70-90% полной емкости ХИТ.
Для R(p) — все наоборот. Чем больше нагрузка и чем сильнее разряжена ячейка, тем больше R(p). Такое поведение R(p) является первопричиной проблем с измерением R(d.c.). Какие элементы конструкции ХИТ определяют R(о) и R(p) — будет показано в следующем пункте.
5) Измерения R(a.c.) на фиксированной частоте 1 кГц — типа, «правильные» и «наше все»
Вообще-то, в англоязычном варианте R(a.c.) есть ни что иное как «Internal Impedance» (внутренний импеданс).
В ГОСТ-Р-МЭК-61557-1-2005 сделан достаточно аккуратный перевод на русский:
 Обратите внимание: «импеданс» vs «сопротивление» и даже буковками обозначено разными (Z vs R). Наверное, что бы не путали теплое с мягким.
Обратите внимание: «импеданс» vs «сопротивление» и даже буковками обозначено разными (Z vs R). Наверное, что бы не путали теплое с мягким.А вот в русскоязычных ГОСТах на аккумуляторы и батарейки — все по-простому. Есть некое «внутреннее сопротивление» ХИТ и меряют его 2 способами: на постоянном токе R(d.c.) или на переменном токе R(a.c.). Причем, «импеданс приблизительно равен сопротивлению».
ГОСТ Р МЭК 61960-3-2019 (ранее — ГОСТ Р МЭК 61960-2007):
 Какому-такому «сопротивлению»? Или R(a.c.)≈R(d.c.) [если я правильно понял тайный смысл примечания от составителей родного ГОСТа].
Какому-такому «сопротивлению»? Или R(a.c.)≈R(d.c.) [если я правильно понял тайный смысл примечания от составителей родного ГОСТа].Давайте посмотрим, насколько R(a.c.) «примерно равно» R(d.c.).
Берем 2 корейских даташита на литий-ион 18650.
Первый — Samsung INR18650-25R. Оказывается, 13 мОм ≈ 22 мОм. Так и запишем…
 Второй — LG 18650HE4, в миру — «банан» из-за специфической расцветки. Здесь 14 мОм ≈ 24 мОм. Прелестно.
Второй — LG 18650HE4, в миру — «банан» из-за специфической расцветки. Здесь 14 мОм ≈ 24 мОм. Прелестно. Ну и ладно. В конечном итоге, уже разобрались, что измерения R(d.c.) — это неблагодарное занятие. А вот мерять R(a.c.) на фиксированной частоте 1 кГц — «и хорошо, и правильно, и куда точнее измерений R(d.c.)». [Кто автор этой сентенции — мне не ведомо.].
Ну и ладно. В конечном итоге, уже разобрались, что измерения R(d.c.) — это неблагодарное занятие. А вот мерять R(a.c.) на фиксированной частоте 1 кГц — «и хорошо, и правильно, и куда точнее измерений R(d.c.)». [Кто автор этой сентенции — мне не ведомо.].Давайте разберёмся, что есть измерение импеданса на фиксированной частоте (1 кГц или иной) и какую полезную информацию оно несет о богатом внутреннем мире ХИТ вообще и о внутреннем сопротивлении в частности.
На самом деле, на ресурсе давно как присутствует статья по этому поводу. Но она слишком большая, слишком подробная и давно забыта.
Надеюсь, что такое импеданс читателю известно. В нулевом приближении эквивалентная схема [замещения] любого ХИТ может быть представлена следующим образом:
 На самом деле, полные эквивалентные схемы реальных аккумуляторов и батареек несколько сложнее. К примеру, для литий-ионного аккумулятора что-то типа такого:
На самом деле, полные эквивалентные схемы реальных аккумуляторов и батареек несколько сложнее. К примеру, для литий-ионного аккумулятора что-то типа такого: Что такое W (элементы Варбурга) и почему в трех случаях емкости были заменены на CPE (элементы постоянной фазы) — желающие могут глянуть в той самой большой статье.
Что такое W (элементы Варбурга) и почему в трех случаях емкости были заменены на CPE (элементы постоянной фазы) — желающие могут глянуть в той самой большой статье.Но на самом деле, все эти ужасы нам не нужны. Для дальнейшего изложения вполне подойдет эквивалентная схема чуть сложнее первой.
Давайте представим (в порядке бреда), что у нас есть приборчик а-ля Hioki CHEMICAL IMPEDANCE ANALYZER IM3590.
 Это тоже измеритель импеданса, типа всенародно-доступных YR1030/1035/1035+ и подобных. Но есть несколько небольших [шутка юмора] отличия:
Это тоже измеритель импеданса, типа всенародно-доступных YR1030/1035/1035+ и подобных. Но есть несколько небольших [шутка юмора] отличия:— IM3590 меряет импеданс ХИТ не на строго определённой частоте (1 кГц), а в широком интервале (1 mHz to 200 kHz), т.е. снимает спектр
— для анализа позволяет использовать эквивалентные схемы
— стоит как крыло от самолета.
Вот, к примеру, берем какой-нибудь литий-ионный аккумулятор (из статьи в журнале «Электрохимия», 2009, №1, с. 42-48) и смотрим этот самый импедансный спектр. В данном случае он представлен как годограф в координатах Найквиста, но не суть. С большой вероятностью стрелки указывают не на конкретные точки 1 кГц, 100Гц и т.д., а на области порядков частот.
 Делаем его «расшифровку» (подробно — в той самой большой статье). И получаем примерно такое.
Делаем его «расшифровку» (подробно — в той самой большой статье). И получаем примерно такое. 
 Наибольший интерес представляют 2 точки:
Наибольший интерес представляют 2 точки:1) Пересечение годографа с осью «Х». R(о) = 33 мОм
2) Пересечение второй окружности с осью «Х». R(d.c.) = R(о)+R(p) = 47 мОм
Некоторые замечания.
► Если повезет, и пересечение годографа с осью «Х» случится при 1 кГц (или сильно рядом), то поздравляю — Вы теперь знаете R(о). Одно плохо — это всего лишь часть активного сопротивления ХИТ.
► Как узнать повезло или не повезло? Да никак. Стрельба по мишени с завязанными глазами.
Примеры непопаданий при 1 кГц на ось Х





► Еще один момент. В импедансометрах используется синусоидальное напряжение с малым размахом: единицы-десятки мВ. В результате — синусоида тока имеет размах не более десятков мА.
 Смысл столь малых нагрузок — исследование системы в состоянии, близком к равновесному. Поэтому измеренные значения R(о) = 33 мОм, R(p) = 47-33 = 14 мОм и общее активное сопротивление R(о)+R(p) = 47 мОм соответствуют сверхмалой нагрузке на ячейку. Что же произойдет, если через ячейку будут протекать токи в сотни мА или еще больше? R(о) — практически не изменится, на то оно и «омическое»;). А R(p) увеличится. Соответственно увеличится и активное сопротивление (см. выше пример с Энелупом). Причем, R(a.c.,1kHz) — это всего лишь некоторая часть R(о)+R(p). В общем случае неизвестная. Если не заморачиваться с дополнительными замерами. А если заморачиваться, то R(a.c.,1kHz) становится не нужным.
Смысл столь малых нагрузок — исследование системы в состоянии, близком к равновесному. Поэтому измеренные значения R(о) = 33 мОм, R(p) = 47-33 = 14 мОм и общее активное сопротивление R(о)+R(p) = 47 мОм соответствуют сверхмалой нагрузке на ячейку. Что же произойдет, если через ячейку будут протекать токи в сотни мА или еще больше? R(о) — практически не изменится, на то оно и «омическое»;). А R(p) увеличится. Соответственно увеличится и активное сопротивление (см. выше пример с Энелупом). Причем, R(a.c.,1kHz) — это всего лишь некоторая часть R(о)+R(p). В общем случае неизвестная. Если не заморачиваться с дополнительными замерами. А если заморачиваться, то R(a.c.,1kHz) становится не нужным.
► Второй интересный момент. Есть мнение что для «обычных» литий-ионных аккумуляторов условие R(о)≈R(a.c.,1kHz) нередко соблюдается. Для Li/LiFePO₄ — вроде как нет. Та же самая Hioki на голубом глазу заявляет: «Этот сигнал переменного тока обычно имеет фиксированную частоту 1 кГц...» и приводит идеализированную картинку (правда, забывает уточнить, что такое бывает в случае литий-иона, да и то не всегда)
 А вот продолжение: "… хотя некоторые продукты позволяют изменять частоту. В последнее время все больше и больше производителей предпочитают проводить испытания внутреннего сопротивления на нескольких частотах, чтобы более эффективно обнаруживать дефектные элементы."
А вот продолжение: "… хотя некоторые продукты позволяют изменять частоту. В последнее время все больше и больше производителей предпочитают проводить испытания внутреннего сопротивления на нескольких частотах, чтобы более эффективно обнаруживать дефектные элементы."Суть в том, что Hioki производит импедансометры как для фиксированной частоты 1 кГц, так и позволяющие снимать спектр. А продавать надо и то и другое.;)
► И еще один интересный момент. В ходе горячего обсуждения очередного «измерителя внутреннего сопротивления аккумуляторов» на 1 кГц был пост ув. virus_59, в коем меня заинтересовал один момент:
Да и внутреннее сопротивление это не гарантия того, что аккумулятор может выдать большой ток. Сам столкнулся с таким на новых китайских 21700 из воздуходувки (и ёмкость не 5Ач, а 3Ач). Вроде и сопротивление в районе 15 мОм, но на 20А просадка с 4,2 до 2,7.Суть данного наблюдения virus_59: китайцы каким-то образом умудрились слепить литий-ионные аккумуляторы, у которых R(p) шибко сильно зависит от величины нагрузки.
Настоящие Самсунги спокойно и 30А держат.
Поэтому правило «чем меньше импеданс R(a.c.,1kHz) — тем больше высокотоковость» в ряде случаев может и не выполняться. Даже для литий-иона. Про остальные ЭХ системы вообще молчу. А кто сказал, что будет легко? :)
6) Имеет ли смысл измерять R(a.c.,1kHz)?
Конечно имеет. Ибо на безрыбье и рак… сами понимаете. Только учитывать некоторые моменты, изложенные выше. Применительно к данной статье: R(a.c.) LR44, измеренное посредством YR1035, безусловно будет отличаться от активного сопротивления R(о)+R(p). Но вряд ли будет отличаться больше чем на порядок. Это с запасом.
Объект исследования, что и как делалось
После предыдущих измерений (часть1, часть2) осталось 4 штуки LR44 Epilso.
 Они были помещены в держатели с припаянными резисторами ~ 680 Ом и подвергнуты дробному разряду.
Они были помещены в держатели с припаянными резисторами ~ 680 Ом и подвергнуты дробному разряду. Суть в следующем:
Суть в следующем:— батарейки разряжались некоторое время (от 4 до 12 ч.)
— затем изменялось напряжение на клеммах под нагрузкой
— потом батарейки вынимались из держателей, производились замеры импеданса и разности потенциалов без нагрузки. Но не сразу, а по истечении 30-60 мин., когда все более-менее устаканится (деполяризация ячейки).
Подробные разрядные кривые, полученные ранее
Аккуратные разрядные кривые для сабжевых «таблеток» были сняты ранее и представлены ТУТ. Причем, с троекратным повторением. Кривые практически единообразны. К примеру, вот кривая, полученная в опыте №1:
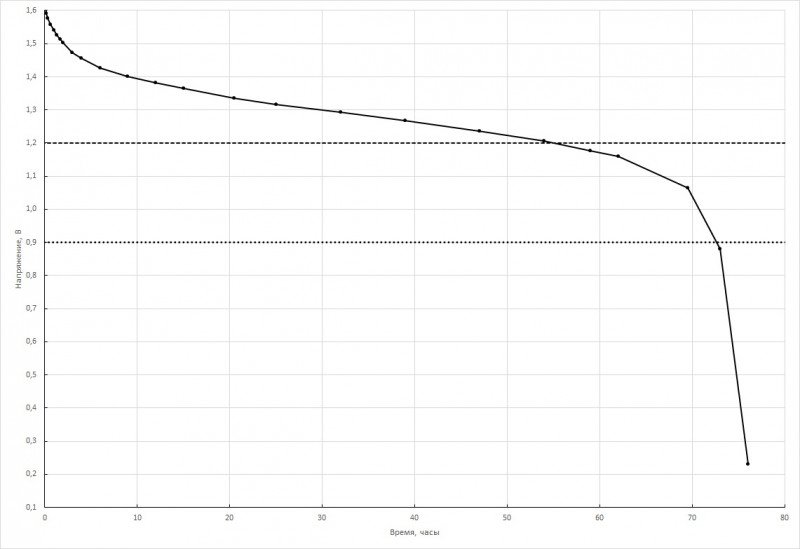

Но смысл данной статьи — не в разрядных кривых.
А в том, что же происходит с импедансом ячеек LR44 в процессе их разряда?
Насколько заметно он увеличивается на различных стадиях разряда?
Что имеем изначально (прямо из блистера)
НРЦ (напряжение разорванной цепи) и импедансы ячеек весьма единообразны.

Результаты эксперимента
Если совсем кратко, то как-то так:
 Пунктирные линии — для U под нагрузкой. Сплошные — НРЦ после «отдыха» 30-60 мин, когда импеданс более-менее стабилизируется. Разница только в координатах экспериментальных точек по оси абсцисс.
Пунктирные линии — для U под нагрузкой. Сплошные — НРЦ после «отдыха» 30-60 мин, когда импеданс более-менее стабилизируется. Разница только в координатах экспериментальных точек по оси абсцисс.Более подробно — под спойлером.
Графики под нагрузкой и без по-отдельности + Таблички исх. данных
Под нагрузкой
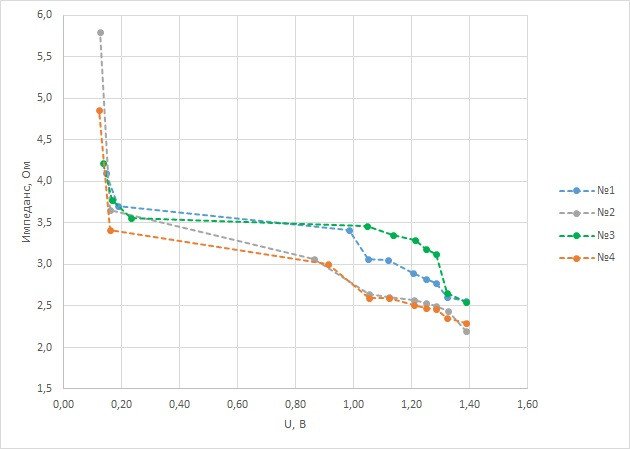 После отдыха
После отдыха
 По образцам
По образцам
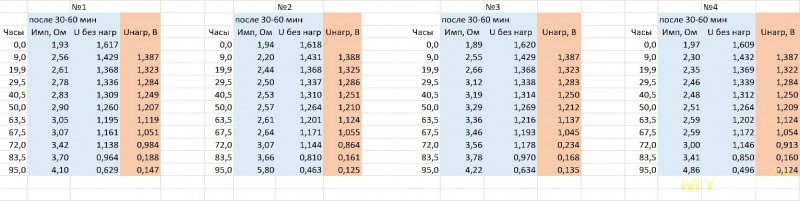
 После отдыха
После отдыха По образцам
По образцам
Еще один вариант представления: какие значения импеданса примерно соответствуют участкам на разрядной кривой. Может, кому-то так будет более понятно.

Заключение
Судя по
Если предположить, что измеряемые значения импеданса LR44 Epilso отличаются от т.н. «внутреннего сопротивления» не более чем на порядок, то в расчётах емкости
Емкость = I·t = (U/R)·t
величиной r можно пренебречь. R = Rн + r ≈ Rн, Rн — сопротивление нагрузочного резистора. А емкость батареек на отсечках 1.2В и 0.9В при Rн = 680 Ω ТУТ и ТУТ определена достаточно корректно.
P.S. Когда материал был уже готов к публикации, я таки придумал как экспериментально оценить насколько сильно импеданс (1 кГц) LR44 отличается от общего активного сопротивления при Rн=680 Ω. Может, всего в 1.5-2 раза, а не на целый порядок? Оказалось, что мой пессимизм был обоснован. Или я что-то делал не так. Подробности под спойлером.
Попытка оценки величины --активного сопротивления--
Измерения выполнены на «таблетке» LR44 Космос, т.к. все Epilso к тому времени были израсходованы.
Разряд осуществлялся в течении 2 часов, в конце были сделаны замеры силы тока и напряжения.
 Затем холдер с «таблеткой» был отключен от нагрузки и началась деполяризация ячейки. Посредством YR1035 несколько раз были сняты значения U и R(a.c.,1kHz).
Затем холдер с «таблеткой» был отключен от нагрузки и началась деполяризация ячейки. Посредством YR1035 несколько раз были сняты значения U и R(a.c.,1kHz).
Что в результате:
1) Деполяризация ячейки
 2) Табличка
2) Табличка
 Расчет активного сопротивления:
Расчет активного сопротивления:
r = (U-U(2час))/(I(2час)-0) = (U-1,4679)/(2,159*0.001)
Подробности (для интересующихся).
1) Был использован держатель для «таблеток» с уже припаянным резистором Rн=677.9Ω. Контакты разорваны — там есть зазор.

2) С одной стороны резистор был отпаян и на это место была припаян кусочек многожильного медного провода (для удобства подключения вольтметра и амперметра). Для данной цепи дополнительное сопротивление ~1мΩ — это просто смешно, учету не поддается.
 На то, что YR1035 показывает некие 0.1 мВ (замер куска провода) — не обращайте внимания. Это глючёк, живет в моем YR1035 уже несколько лет и ни на что не влияет.;)
На то, что YR1035 показывает некие 0.1 мВ (замер куска провода) — не обращайте внимания. Это глючёк, живет в моем YR1035 уже несколько лет и ни на что не влияет.;)
3) Дополнительное сопротивление, которое добавляет амперметр. Точнее — общее сопротивление щупов с проводами + шунт. Есть 2 варианта подключения (как и на всех вменяемых мультиметрах): «до 10А» и «до 400мА»
 Был выбран второй способ, ибо разрешение в «мА» на 2 порядка больше.
Был выбран второй способ, ибо разрешение в «мА» на 2 порядка больше.
В результате получается R внешней цепи 678Ω+2Ω=680Ω. Прямо, как доктор прописал. Но это чистое совпадение и погоды не делает.
4) Подключение
 В дальнейшем оказалось, что мультиметр HP-37C вполне логично заменить на YR1035 и получить один дополнительный разряд справа. Ибо:
В дальнейшем оказалось, что мультиметр HP-37C вполне логично заменить на YR1035 и получить один дополнительный разряд справа. Ибо:
— разрешение по напряжению на порядок больше, чем у HP-37C
— показания U на YR1035 совпадают с таковыми для Флюка 287(тут)

Разряд осуществлялся в течении 2 часов, в конце были сделаны замеры силы тока и напряжения.
 Затем холдер с «таблеткой» был отключен от нагрузки и началась деполяризация ячейки. Посредством YR1035 несколько раз были сняты значения U и R(a.c.,1kHz).
Затем холдер с «таблеткой» был отключен от нагрузки и началась деполяризация ячейки. Посредством YR1035 несколько раз были сняты значения U и R(a.c.,1kHz).Что в результате:
1) Деполяризация ячейки
 2) Табличка
2) Табличка Расчет активного сопротивления:
Расчет активного сопротивления: r = (U-U(2час))/(I(2час)-0) = (U-1,4679)/(2,159*0.001)
Подробности (для интересующихся).
1) Был использован держатель для «таблеток» с уже припаянным резистором Rн=677.9Ω. Контакты разорваны — там есть зазор.

2) С одной стороны резистор был отпаян и на это место была припаян кусочек многожильного медного провода (для удобства подключения вольтметра и амперметра). Для данной цепи дополнительное сопротивление ~1мΩ — это просто смешно, учету не поддается.
 На то, что YR1035 показывает некие 0.1 мВ (замер куска провода) — не обращайте внимания. Это глючёк, живет в моем YR1035 уже несколько лет и ни на что не влияет.;)
На то, что YR1035 показывает некие 0.1 мВ (замер куска провода) — не обращайте внимания. Это глючёк, живет в моем YR1035 уже несколько лет и ни на что не влияет.;)3) Дополнительное сопротивление, которое добавляет амперметр. Точнее — общее сопротивление щупов с проводами + шунт. Есть 2 варианта подключения (как и на всех вменяемых мультиметрах): «до 10А» и «до 400мА»
 Был выбран второй способ, ибо разрешение в «мА» на 2 порядка больше.
Был выбран второй способ, ибо разрешение в «мА» на 2 порядка больше.В результате получается R внешней цепи 678Ω+2Ω=680Ω. Прямо, как доктор прописал. Но это чистое совпадение и погоды не делает.
4) Подключение
 В дальнейшем оказалось, что мультиметр HP-37C вполне логично заменить на YR1035 и получить один дополнительный разряд справа. Ибо:
В дальнейшем оказалось, что мультиметр HP-37C вполне логично заменить на YR1035 и получить один дополнительный разряд справа. Ибо:— разрешение по напряжению на порядок больше, чем у HP-37C
— показания U на YR1035 совпадают с таковыми для Флюка 287(тут)

И на этом все. Всего доброго.
Самые обсуждаемые обзоры
| +69 |
3008
109
|
| +55 |
3262
36
|
…
А в это время китайские инженеры торопливо переписывают графики и текст себе в блокнотик.
Если штангель не начинает глючить вплоть до 0.9-1.0В на LR44, то можно ориентироваться на ёмкость примерно150-170 мАч.
А если 1.2В для него уже предел — то где-то 100-110 мАч.
Спасибо за труд.
1) немного не понятна логика того что две трети заметки описывается почему мерять 1кГц не правильно, а все-таки надо спектр снимать, а потом мерятся все на 1кГц, но ладно сошлемся на объяснение «Ибо на безрыбье и рак… сами понимаете.» OK, ситуация понятна, но но измерение чего происходит все еще не понятно
2) Я так и не понял какие выводы можно сделать из этих измерений? Что импеданс растет высаживании батареек? Ну это логично и давно изучено. Как он растет при высаживании батареек? Ну тут миллион параметров, которые могут влиять на импеданс по почти не влиять на эксплуатационные качества элемента. Мало того, если цель попытаться найти тенденции изменения импеданса то вероятно надо было исследовать несколько видов элементов от разных производителей… В общем загадка. Я не хочу обидеть или оскорбить уважаемого автора не в коем разе, но все равно не понял
А если так, то какая разница, точно ли вы измерили эту величину или нет? Ведь измеренное значение будет актуально только для ваших условий разряда. Получается, что точность самой методики не очень-то и важна, ведь единственное, для чего мы можем применять полученные результаты — это сравнение разных элементов, и здесь просто важно, чтобы методика измерений была всегда одна и та же, и вот именно для этого её и прописали в ГОСТ.
По сути, один-в-один с измерением импеданса с помощью YR1035 — результаты напрямую тоже неприменимы, но можно сравнивать разные элементы.
1) Почему все так любят мерять мостовой импеданс на 1кГц и делать из него какие-то выводы? Существует миллион причин которые влияют на импеданс 1кГц, при этом оказывая минимальное влияние на эксплуатационные характеристики, включая проблемы с соединением выводов к подложке электродов (привет тесла), проблемы с толщиной подслоя (привет панасоник), толщиной и равномерностью самих активных масс, качеством сепараторов, равномерностью размера частиц и тд и тп. Даже на очень зрелых процессах получить два одинаковых элемента практически невозможно, да и не нужно. Мало того, импеданс (причем не на 1кГц, а подгоняющийся под строго под данный элемент) используется только для первичной отбраковки и на производстве вообще не несет никакого смысла.
Если мы хотим сделать какие-то выводы об элементе вообще, то нужно уже снимать полноценные спектры импеданса, причем с разной амплитудой, и желательно как сделал автор — при разной степени разряда. А после этого их отфитовать и получить отдельно значения CPE и R в каждой части спектра. А если хочется чуть больше информации — то вообще в процессе разрядки. При этом количество информации будет ограничено, и вы все равно не сможете сказать ВСЕ об этом элементе. На практике это работа на несколько месяцев без учета времени и трудоемкости самих измерений (их будет делать кастомный стенд). Зачем это нужно пользователю (пусть даже очень продвинутому, не говоря об обычном) я не знаю.
На практике нормальные производители просто приводят гарантированные характеристики элементов, и пользователь волен выбирать нужный элемент под свои нужды.
Цена вопроса — 2830руб (включая НДС). Возможен бартер на б/у Стремянко люминиевая Barneo ST24 с Вашей доплатой.
ЗЫ. Если я правильно понял тайный смысл Вашего замечательного поста.
Не очень понятно, почему автор столь упорно избегает термина «дифференциальное сопротивление» (собственно, о котором тут идет речь в 80% случаев) — чтобы не испугать читателя? Еще больше?)
Ну и в ГОСТ нет никакого противоречия. Измерение тока и напряжения на переменном токе — по сути, действительно приводит к измерению импеданса, так как реактивный характер цепи (см. емкости в эквивалентной схеме) приводит к сдвигу фазы тока относительно напряжения. Но на частоте 1 кГц этот сдвиг достаточно невелик, чтобы им можно было пренебречь на практике. Что, кстати, видно на годографе.
иногда (исключающе редко) и такое требуется :)
Ничего личного. Навеяло
Не понял, зачем я это написал…
И далее по рекурсии.
Если вы пришли только проявить неуважение к труду автора, то может, было бы добрее просто пройти стороной.
Закон Ома как бэ предполагает деление напряжения на ток в одной временной точке. Как можно делить текущее напряжение на ток из прошлого? Нет, я понимаю вашу идею — типа, всё поляризационное падение напряжения вы ассоциировали с внутренним сопротивлением, поэтому, истинное напряжение элемента — то, к которому оно вернется спустя время после снятия нагрузки. Но это же не так работает — вот намеряли вы 22 Ома в итоге, но ведь если бы вы замерили ток КЗ элемента сразу после окончания разряда, вы бы получили значение больше 67 мА (емнип ток КЗ LR44 больше 100 мА), значит, нет там такого сопротивления даже временно.
Отнюдь. Закон Ома — это не про деление напряжения на ток в одной точке. Он про линейную зависимость тока от напряжения в некотором интервале напряжений. Как правило — достаточно продолговатую по напряжению. Объекты, более-менее хорошо подчиняющиеся той зависимости называются «линейными» или «омическими».
Какого-такого «прошлого»?:)
Текущее напряжение — это под нагрузкой, на языке электриков и радиолюбителей — «просаженное». Ежели поделить Uтекущее/Iтекущий, то получится R «внешней цепи». Это всяко-разная ботва (Rн + Rшунта + Rпроводов+кракодилов)… Но там нет т.н. Rвн.
А порядок Rвн можно можно оценить по величине той самой «просадки». Осложнением является т.н. явление деполяризации. Ибо оно [в идеале — бесконечно] весьма продолговато по времени и является следствием асимптотического возврата системы в состояние равновесия.
Вот и вся логика концовки статьи.
Я бы мог как раз предложить оценивать Rвн по току КЗ, но, опять же, не уверен, что мы получим достоверные значения. Как я понимаю, как Rвн, так и емкость меняются в зависимости от условий разряда, а, значит, гнаться за их точным вычислением бессмысленно, т.к. это будет актуально только для измеряемого режима. То есть, оба этих параметра можно лишь использовать для сравнения разных элементов.
Автор взял батарейки разного срока выпуска. Которые по разному хранились. По одному экземпляру. Ни у кого не было — купили упаковку одинаковых батареек, одни работают нормально, а несколько штук глючные? Чтобы делать достоверные выводы, нужно проверить партию одинаковых. А что у автора? Все эти графики и параметры относятся к конкретному экземпляру батарейки, которая попалась автору. Да к тому же и замеры сделаны некорректно.
Потрудился он конечно
хорошомного, Но практический смысл?Но светлое будущее еще не наступило, и от этой мелочи питаются устройства с микромощным стабильным потреблением.
100 мАч = 360 Кл
Про график расчета сопротивлегия на постоянном токе: у вас при больших токах меньшее сопротивление. Это не ошибка? Значит Rp отрицательное и не линейно?
1) Rp всегда нелинейно зависит от нагрузки и уровня заряда ХИТ. Это общеизвестно.
2) Rp не бывает отрицательным. Как и любые другие R.
Тема названа… «Изменение импеданса (1 кГц) LR44...»
Смотрим, что это?
Формфактор LR44
Химический тип Щелочная (алкалиновая)
Типоразмер LR1154, AG13, V13GA, А76, 357
Номинальное напряжение, В 1.5
Это Батарейка LR44 (GP A76F-2C10) — Марганцево-цинковые дисковые алкалиновые батарейки.
Исследование проведены на батарейке.
Я даже сначала не понял, зачем это сделано?
Ну сделано. Ладно.
Я причем тут аккумуляторы с другой химией вообще?
Что автор сравнивает?
Букв много.
Но оно о разном…