YR1035 – импедансметр на частоте 1 кГц. Часть II. Про внутреннее сопротивление гальванических элементов

- Цена: US $53-69 , брал за 65
- Перейти в магазин
Это вставка в ОБЗОР. Нумерация разделов и пунктов соответствует части I.
Disclaimer (отмазка): основной целью написания Части II являлось желание самому разобраться в том, что удалось накопать за несколько месяцев. Не уверен, что это следовало публиковать (тем паче на Муське), но угробить столько времени для «писанины в стол» тоже как то глупо. Если получилось слишком запутанно и громоздко — так и сам предмет рассмотрения один из наиболее мутных в электрохимии.
В начале приведен краткий список литературы. Первоисточники выложены в облако, искать не надо.
0. СЛОВАРИК аббревиатур и терминов
ХИТ — химический источник тока. Бывают гальванические и топливные. Далее речь идет только о гальванических ХИТ.
Импеданс (Z) – комплексное электрическое сопротивление Z=Z’+iZ’’.
Адмиттанс (А) – комплексная электропроводность, величина обратная импедансу. A=1/Z
ЭДС – «чисто химическая» разность потенциалов между электродами в гальваническом элементе, определяемая как разность электрохимических потенциалов анода и катода.
НРЦ — напряжение разорванной цепи, для одиночных элементов обычно примерно равно ЭДС.
Анод (химическое определение) – электрод, на котором происходит окисление.
Катод (химическое определение) – электрод, на котором происходит восстановление.
Электролит (химическое определение) – вещество, которое в растворе или расплаве (т.е. в жидкой среде) распадается на ионы (частично или полностью).
Электролит (техническое, НЕ химическое определение) – жидкая, твердая или гелеобразная среда, проводящая электрический ток за счет движения ионов. Ежели по-простому: электролит (техн.) = электролит (хим.) + растворитель.
ДЭС — двойной электрический слой. Всегда есть на границе раздела электрод/электролит.
4. Почему внутреннее сопротивление ХИТ на постоянном токе R(d.c.) и переменном токе R(a.c.) разные?
4.1. Вариант №1. Самое простое объяснение
Это даже не объяснение, а как бы констатация факта (взято у Тагановой).
1) То, что измеряется на постоянном токе R(d.c.) – это сумма двух сопротивлений: омического и поляризационного R(d.c.) = R(о) + R(pol).
2) А когда на переменном, да еще на «правильной» частоте 1 кГц, R(pol) исчезает и остается только R(о). То есть, R(1 кГц) = R(о).
По крайней мере, на это хочется надеяться экспертам МЭК, Алевтине Тагановой, а также многим (почти всем), кто измеряет R(d.c.) и R(1 кГц). И путем нехитрых арифметических действий получает R(о) и R(pol) по отдельности.
Если такое объяснение Вас устраивает, то дальше этот раздел можете не читать.
4.2. Вариант №2. Для особо интересующихся
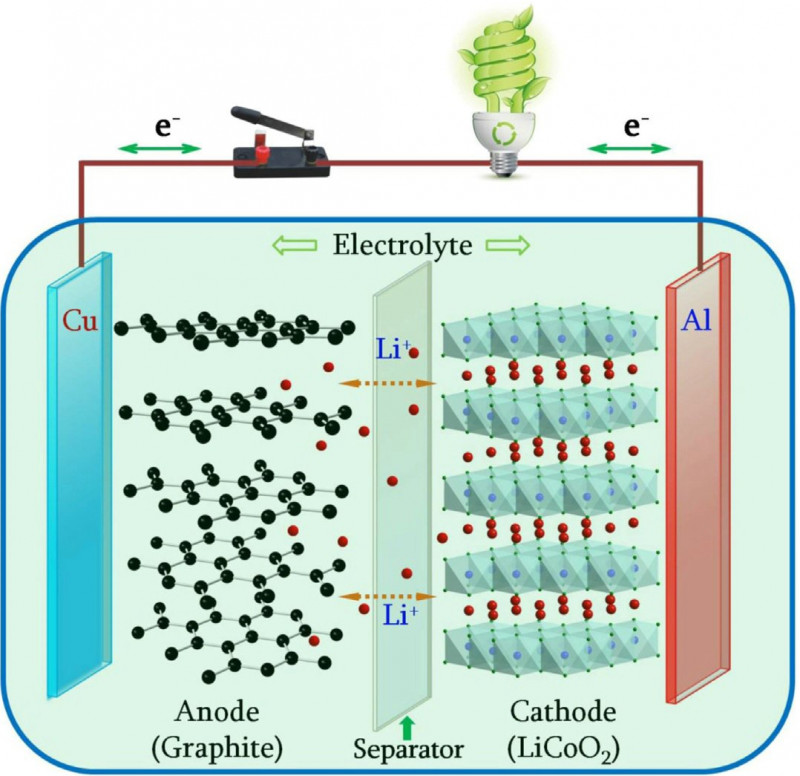
Для начала попробуем схематически изобразить как выглядит богатый внутренний мир одной электрохимической ячейки. Возьмем, к примеру, гальванический элемент, где за перенос электричества во внутренней цепи отвечают ионы лития. Аккумулятор или батарейка – без разницы. На аккумуляторе может быть написано «Li-ion» или «Li-polimer» — по барабану.
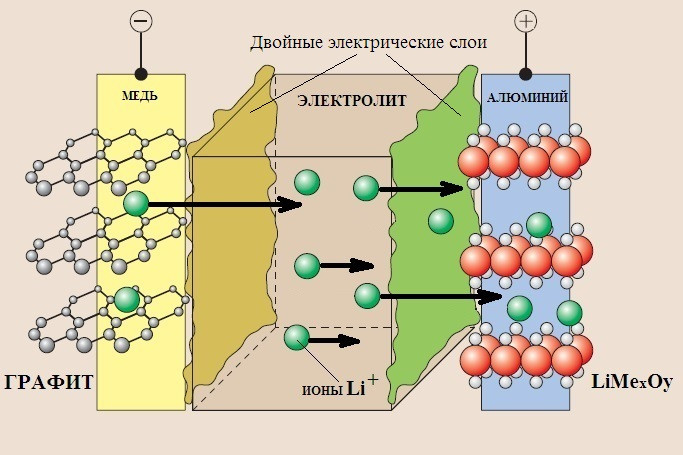 На картинке стрелочками изображено направление движения ионов Li(+) в процессе разряда (и саморазряда) элемента, т.е. когда элемент работает. Слева анод (окисление Li(0) – e(-) = Li(+)), справа катод (восстановление Li(+) + e(-) = Li(0)). Если поставить ХИТ на зарядку обозначения анод-катод поменяются местами. Но не суть.
На картинке стрелочками изображено направление движения ионов Li(+) в процессе разряда (и саморазряда) элемента, т.е. когда элемент работает. Слева анод (окисление Li(0) – e(-) = Li(+)), справа катод (восстановление Li(+) + e(-) = Li(0)). Если поставить ХИТ на зарядку обозначения анод-катод поменяются местами. Но не суть.
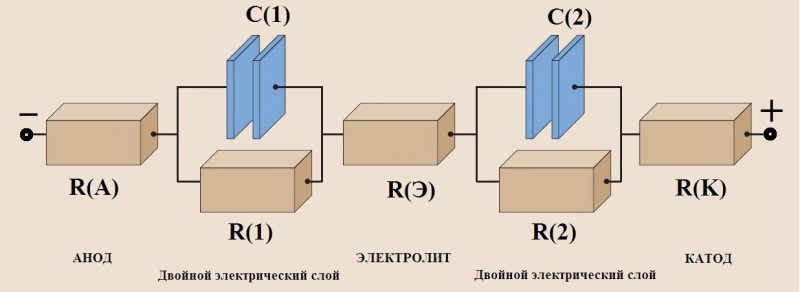
Попробуем изобразить гальванический элемент в виде эквивалентной электрической цепи. Я тут набросал схемку. Все элементы этой схемы незримо присутствуют во всех ХИТ. Зачастую, весьма странно видоизменяясь. Но это сейчас не важно. Частности, нюансы, дополнительные усложнения пока опущены.
 или
или
R(A)+R(1)/C(1)+R(Э)+R(2)/C(2)+R(K)
Строка выше – это не арифметическое выражение. Это краткая запись структуры, изображенной на рисунке.
Основные составляющие этой схемы вроде как понятны. Кроме одного: что такое двойной электрический слой (ДЭС)?
Вообще говоря, ДЭС – штука довольно распространенная как в природе, так и в технике. Так как каждый из электродов гальванического элемента заряжен, то на его поверхности всегда есть слой «прилипших» противоионов (ионов со знаком заряда, обратным заряду электрода) из раствора электролита. Вот картинка из некой диссертации по морфологии почв. Только слова «глинистая частица» нужно заменить на «электрод»:
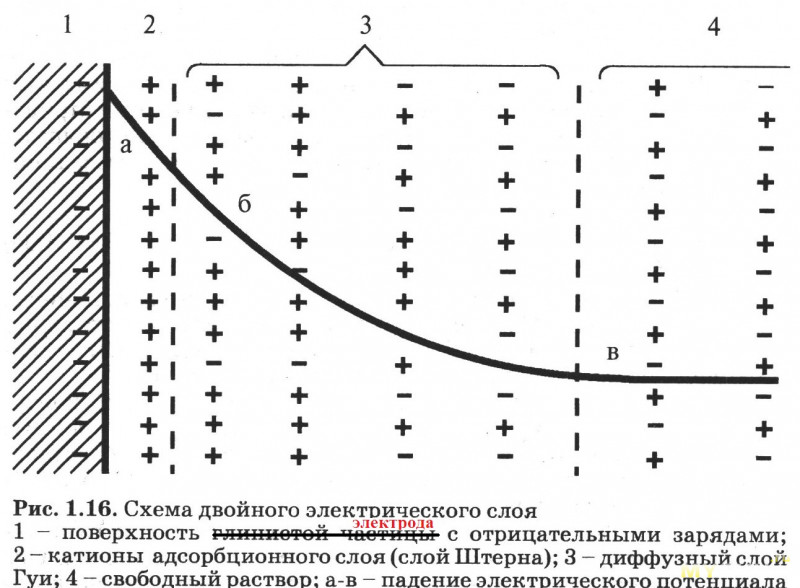 Относительно слоев Штерна и Гуи можите не забивать себе голову – это Вам никогда не пригодится.
Относительно слоев Штерна и Гуи можите не забивать себе голову – это Вам никогда не пригодится.
При прохождении тока, ДЭС ведет себя подобно конденсатору с очень большой утечкой. «Утечка» обусловлена протеканием окислительно-восстановительной реакции на границе раздела электрод-электролит. Все это можно представить в виде эквивалентной схемы, состоящей из идеального конденсатора С и идеального резистора R. Или, как говорят в нынешней электрохимии, «емкости и сопротивления с сосредоточенными параметрами».
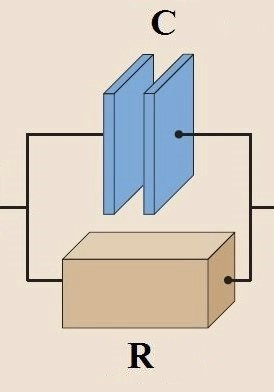 Как известно, для цепей, в которых протекает переменный ток, используется понятие импеданса. Импеданс (комплексное сопротивление) Z определяется как Z=Z’+iZ’’, где Z’ – активная (действительная), а Z” – реактивная (мнимая) составляющие полного импеданса. В координатах Re(Z) — Im(Z) все это выглядит следующим образом:
Как известно, для цепей, в которых протекает переменный ток, используется понятие импеданса. Импеданс (комплексное сопротивление) Z определяется как Z=Z’+iZ’’, где Z’ – активная (действительная), а Z” – реактивная (мнимая) составляющие полного импеданса. В координатах Re(Z) — Im(Z) все это выглядит следующим образом:
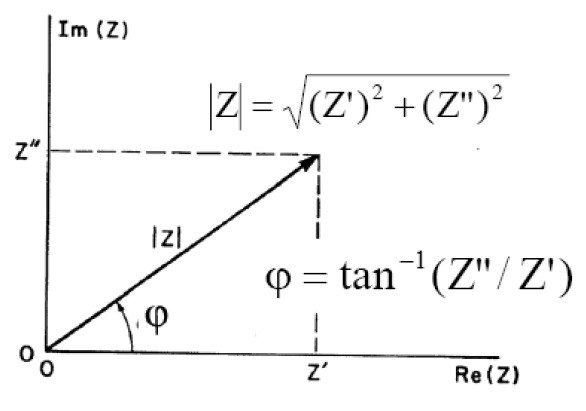 Нетрудно заметить, что Z’ и Z’’ – это проекции импеданса на соответствующие оси.
Нетрудно заметить, что Z’ и Z’’ – это проекции импеданса на соответствующие оси.
Для тех, кто пока не понимает, о чем идет речь – ЗДЕСЬ об этом рассказано предельно просто.
Общеизвестно, что для параллельно соединенных конденсатора и резистора активная и реактивная составляющие определяются выражениями:
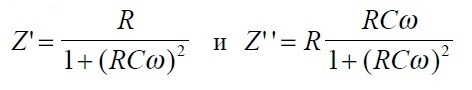 где ω — круговая частота.
где ω — круговая частота.

На практике проще всего сделать измерение активной части импеданса Z’.
В предельных случаях:
а) если частота = 0 (измерения на постоянном токе) то Z’ = R;
б) если частота стремится к бесконечности, то Z’ = 0.
Во втором случае конденсатор ведет себя по отношению к резистору как шунт с сопротивлением, равным нулю. В результате, сопротивление R уже никак не влияет на общее сопротивление цепи.
А что же будет получено между двумя крайними случаями?
Это лучше посмотреть на картинке. Графическая зависимость Z от частоты в координатах (Z’)/-(Z’’) (координаты Найквиста) называется годографом импеданса, или его спектром.
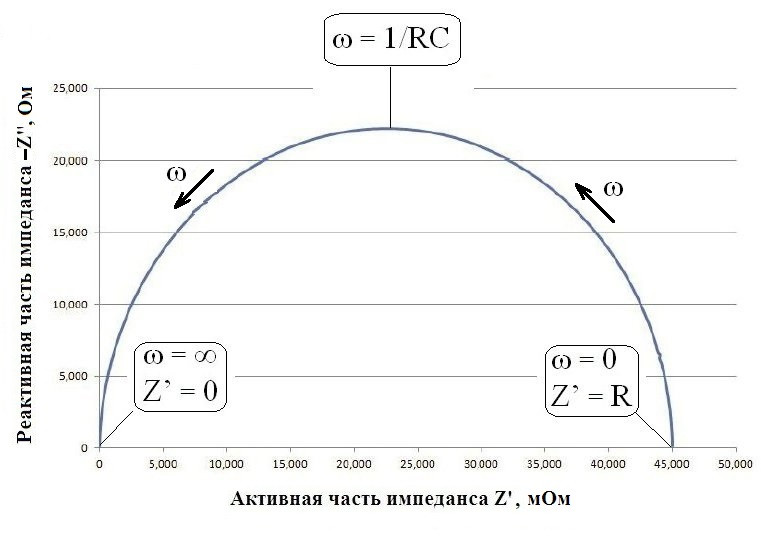 Если на этом полукруге поставить точки через равные промежутки по частоте, то они будут расположены неравномерно, чем выше частота – тем гуще. То есть левая часть кривой стремится к Z’’ = 0 асимптотически.***
Если на этом полукруге поставить точки через равные промежутки по частоте, то они будут расположены неравномерно, чем выше частота – тем гуще. То есть левая часть кривой стремится к Z’’ = 0 асимптотически.***
***Примечание. Только в рамках данной примитивной модели. Годографы реальных литиевых ХИТ выглядят заметно сложнее. И нет там никакого асимптотического приближения. Спектральная кривая Z пресекает ось действительных значений Z и уходит в область положительных значений Z’’ (она внизу). Как пример – годограф некого японского литий-ионного аккумулятора ENAX (ENAX Inc., Tokyo, Japan) “High Power Cell” NX2P0M (2.0 Ah)
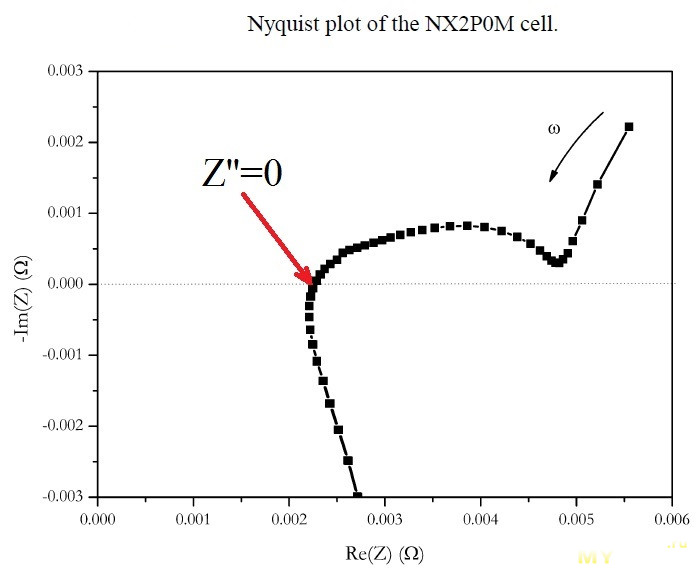 Или вот пример из информационного листка «EC-Lab — Application Note #61» (янв. 2017) с более знакомыми нам испытуемыми:
Или вот пример из информационного листка «EC-Lab — Application Note #61» (янв. 2017) с более знакомыми нам испытуемыми:
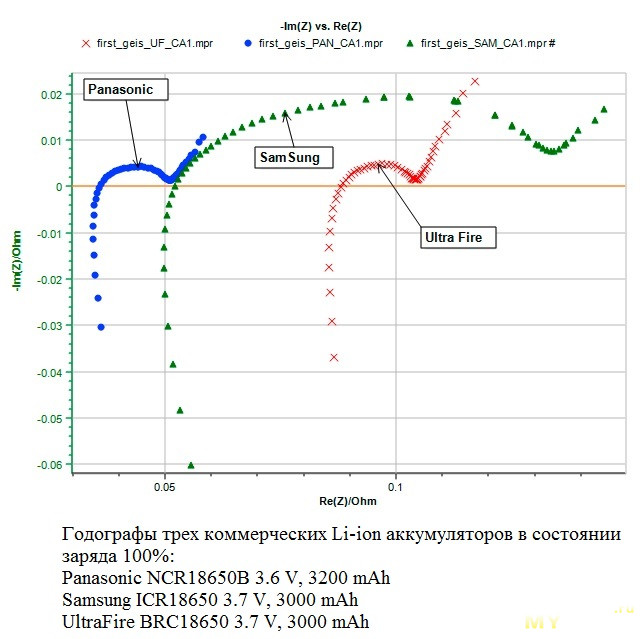 И еще пример для понимания частотных диапазонов из информ. листка «EC-Lab — Application Note #62» (февр. 2017) по измерению внутреннего сопротивления некого Li-ion АКБ:
И еще пример для понимания частотных диапазонов из информ. листка «EC-Lab — Application Note #62» (февр. 2017) по измерению внутреннего сопротивления некого Li-ion АКБ:
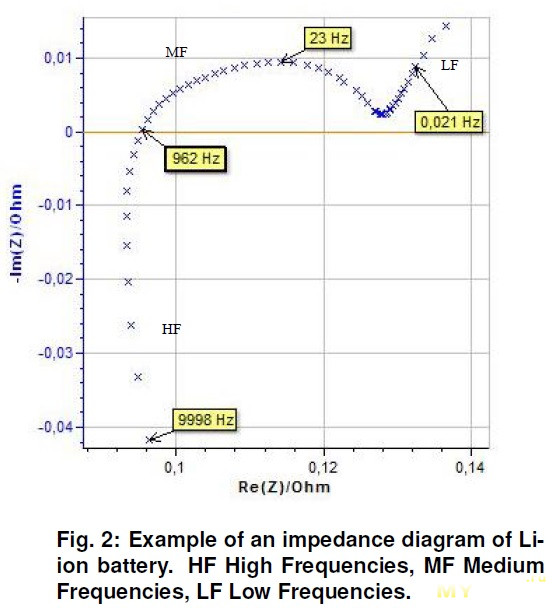
Теперь самое главное.
1) При измерениях внутреннего сопротивления на постоянном токе
R(d.c.) = R(о) + R(pol)
R(d.c.) = R(А) + R(Э) + R(К) + R(1) + R(2)
R(о) = R(А) + R(Э) + R(К)
R(pol) = R(1) + R(2).
2) Если для обоих электродов на частоте 1 кГц выполняется [примерно выполняется] условие Z’’ = 0, то
R(a.c.) = R(о)
R(a.c.) = R(А) + R(Э) + R(К).
Если такое объяснение Вас устраивает, то следующий пункт лучше не читать.
4.3. Продолжение. Для сильно-сильно интересующихся
1) Сами того не подозревая, мы залезли в местами интересный, но весьма заумный метод электрохимии, который называется спектроскопия электрохимического импеданса (СЭИ, EIS).
2) В настоящее время СЭИ считается наиболее мощным методом изучения электрохимических систем. Но, как говорится, есть «маленький нюанс»: однозначная интерпретация результатов в СЭИ – штука весьма затруднительная.
«Реальные электрохимические системы в общем случае являются многомерными, нелинейными, частично необратимыми, большими статистическими системами с распределенными параметрами в макро- и микро масштабе. В них протекают сложные процессы обмена энергии и массы, которые изменяют их параметры и структуры, вследствие чего они способны проявлять себя как нестационарные системы с памятью.» ©
Собственно об этом и будет в данной части изложения. Не так, чтобы сорвать покровы, раскрыть сокровенные тайны и расставить точки над «и». Нет, все намного скромнее – просто приподнять завесу, оценить обстановку в целом и больше туда не соваться…
Если все еще интересно, то продолжим.
RC-элемент был рассмотрен выше. Начинаем потихоньку усложнять модель и наблюдать за изменениями формы и положения годографа в системе координат Найквиста.
4.3.1. Добавляем сопротивление одного из электродов
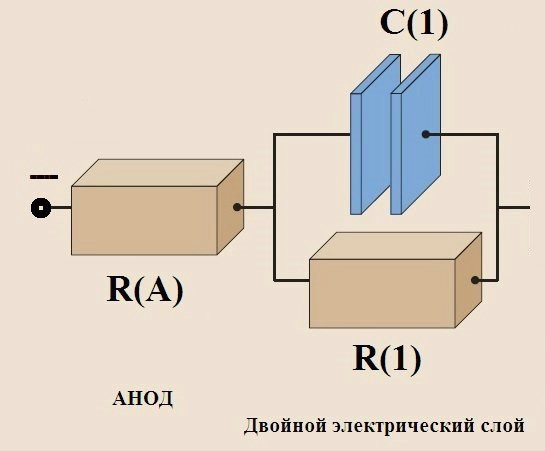 Тут все просто – годограф сдвигается вправо на величину R(A).
Тут все просто – годограф сдвигается вправо на величину R(A).
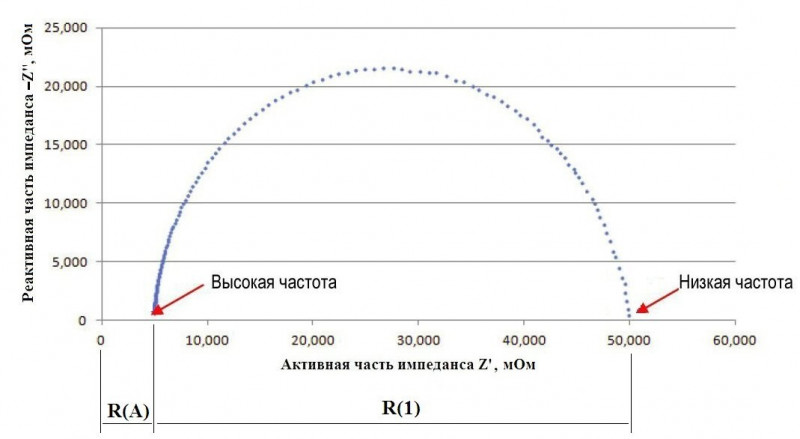
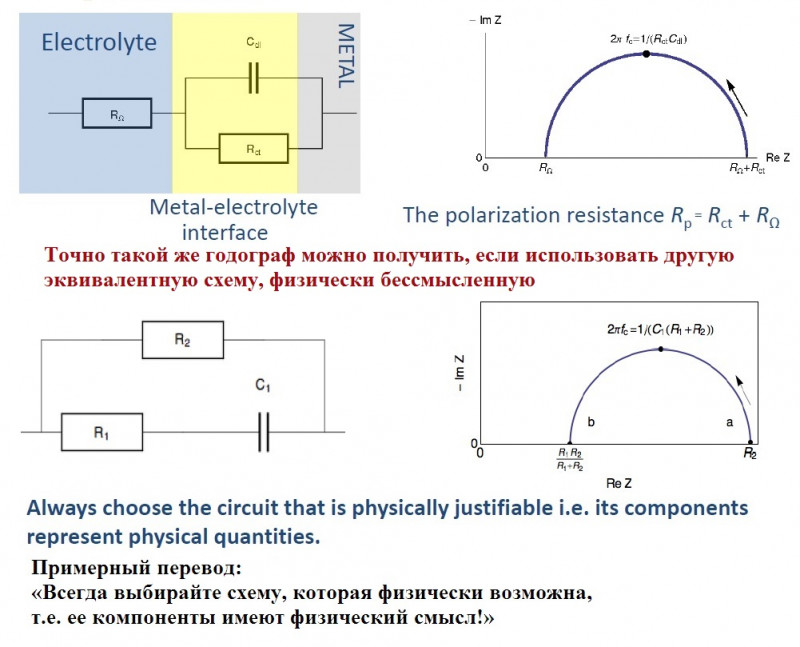
4.3.2. Добавляем электролит.
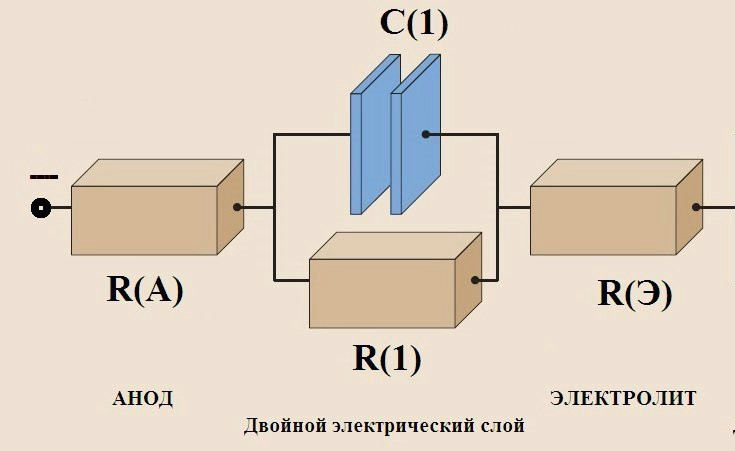 Ну, понятно – годограф еще сдвинется вправо на величину R(Э).
Ну, понятно – годограф еще сдвинется вправо на величину R(Э).
Все верно, сдвигается на R(Э). Но еще на годографе любого ХИТ появляется хвост в области сверхнизких частот (~1 Гц и меньше). Это так называемый диффузионный импеданс.
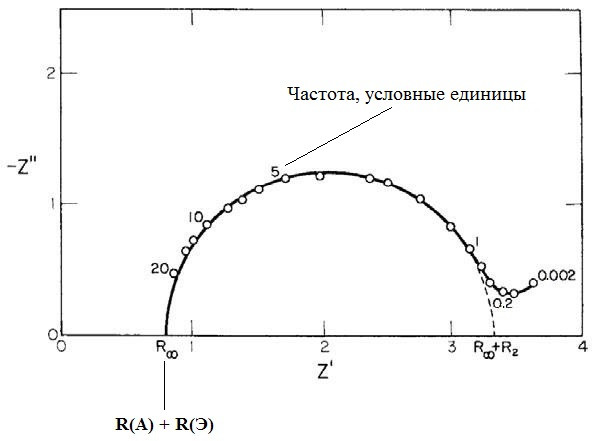 Наличие на годографе хвоста в области очень низких частот было впервые объяснено Варбургом с использованием ряда упрощающих предположений. На самом деле, некоторые из них в реальных ячейках в принципе неосуществимы (например – диффузия из неограниченного объема). Тем не менее, до сих пор диффузионный хвост кривой годографа часто связывают (в нулевом приближении) с диффузионным импедансом Варбурга. Если кратко, то импеданс Варбурга описывается выражением
Наличие на годографе хвоста в области очень низких частот было впервые объяснено Варбургом с использованием ряда упрощающих предположений. На самом деле, некоторые из них в реальных ячейках в принципе неосуществимы (например – диффузия из неограниченного объема). Тем не менее, до сих пор диффузионный хвост кривой годографа часто связывают (в нулевом приближении) с диффузионным импедансом Варбурга. Если кратко, то импеданс Варбурга описывается выражением
 Слово «постоянная» для W(0) означает, что эта величина не зависит от частоты. Но зависит от кучи других факторов: концентрации, температуры и т.д. На самом деле, это не постоянная, а всего лишь коэффициент пропорциональности, не зависящий от одного параметра – частоты.
Слово «постоянная» для W(0) означает, что эта величина не зависит от частоты. Но зависит от кучи других факторов: концентрации, температуры и т.д. На самом деле, это не постоянная, а всего лишь коэффициент пропорциональности, не зависящий от одного параметра – частоты.
Из уравнения выше следует, что Z’/Z’’=1. Поэтому в идеале годограф импеданса Варбурга выглядит очень просто:
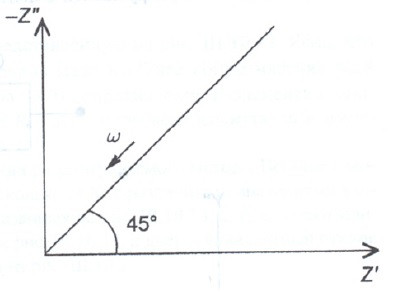 Это означает, что независимо от частоты, ток по фазе опережает напряжение на 45 град.
Это означает, что независимо от частоты, ток по фазе опережает напряжение на 45 град.
Если наложить годограф Варбурга на годограф одного из электродов, то получится вот такая картинка:
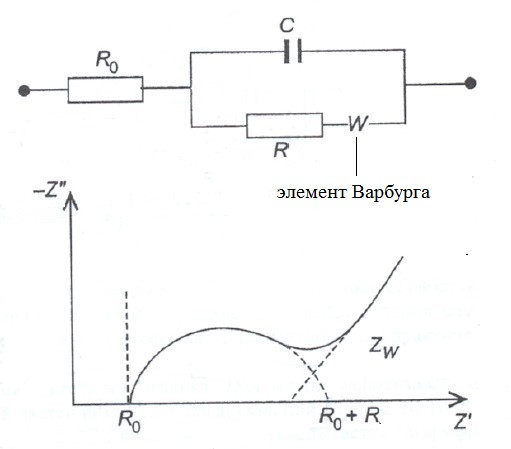 Для реальных электрохимических ячеек все это может выглядить несколько по-иному, но об этом будет ниже.
Для реальных электрохимических ячеек все это может выглядить несколько по-иному, но об этом будет ниже.
И еще один момент – не надо пытаться экстраполировать импеданс Варбурга до частоты, равной 0. Потому что это бессмысленно. На постоянном токе никаких диффузионных импедансов не существует. Есть только омическое сопротивление электролита R(Э).
4.3.3. Как учесть тот факт, что электродов два?
Да очень просто – полуокружности годографов 2-х электродов накладываются друг на друга:
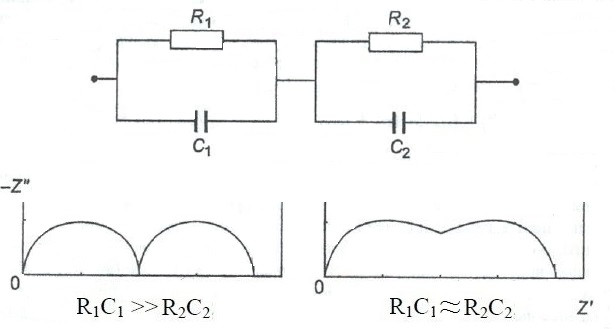 Примечание.На самом деле, годографы, изображенные выше, одинаково хорошо описывают ажник три разные эквивалентные схемы:
Примечание.На самом деле, годографы, изображенные выше, одинаково хорошо описывают ажник три разные эквивалентные схемы:
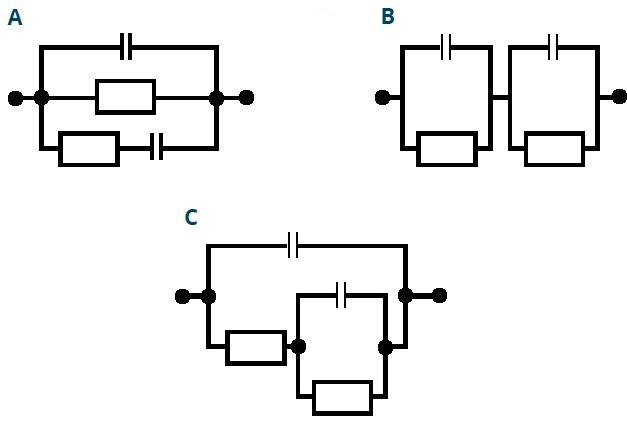 Но сейчас это не важно. Или гляньте, что там под спойлером в п.4.3.1…
Но сейчас это не важно. Или гляньте, что там под спойлером в п.4.3.1…
Ежели «по жизни» — левый годограф (две отдельные полуокружности) в случае реальных ХИТ никогда не наблюдается (лично я не встречал ни разу). А второй вариант — сплошь и рядом. Только это не полуокружности, а дуги (см ниже -«CPE»). Ну и радиусы у них могут быть разные (что вполне естественно). Бывают ситуации, когда две дуги сливаются в одну. Вот пример (выдернул из какого-то мануала по практическому применению метода СЭИ):
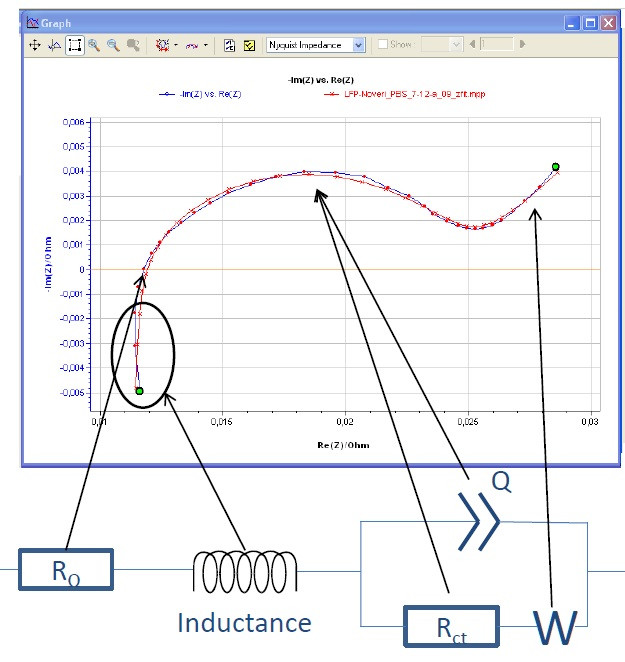 Там 2 кривые: одна экспериментальная, вторая — расчетная по эквивалентной схеме в нижней части рисунка. Про то, откуда появляется индуктивность и про CPE-элемент, обозначенный как «Q», будет рассказано ниже.
Там 2 кривые: одна экспериментальная, вторая — расчетная по эквивалентной схеме в нижней части рисунка. Про то, откуда появляется индуктивность и про CPE-элемент, обозначенный как «Q», будет рассказано ниже.
4.3.4. Что делать, если эксперимент не соответствует простейшим моделям?
В этом случае теоретики обычно говорят: «Тем хуже для эксперимента!». Шутка юмора.
Но на самом деле оказалось, что годографы реальных электрохимических ячеек не укладываются в ложе примитивных построений, изложенных выше. Причем всегда.
Экспериментаторы взвыли: «Дайте нам теоретическое объяснение!».
И теоретики дали почти универсальный ответ: элемент с постоянным сдвигом фазы (СРЕ – constant phase element). Его часто неправильно называют как «элемент постоянной фазы» — лобовой перевод с английского.
А потом добавили «контрольный в голову»: конечный элемент постоянного сдвига фазы (ВСР). И все вопросы с формальным описанием были закрыты. Но проблемы с объяснением многих моментов на уровне физики и химии процессов остались. Но не суть. Пусть с этим разбираются специалисты. Это ихкорм хлеб.
Коротенько про СРЕ.
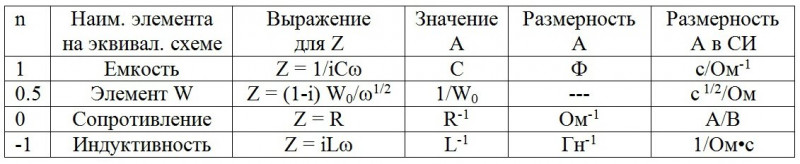
Все очень просто. Импеданс любого структурного элемента на эквивалентных схемах можно представить как частный случай вот такого выражения
 Для целых значений n=1, 0, -1 элемент СРЕ вырождается до классических элементов с сосредоточенными параметрами C, R, L. Для n=0.5 СРЕ дает импеданс Варбурга в чистом виде.
Для целых значений n=1, 0, -1 элемент СРЕ вырождается до классических элементов с сосредоточенными параметрами C, R, L. Для n=0.5 СРЕ дает импеданс Варбурга в чистом виде.
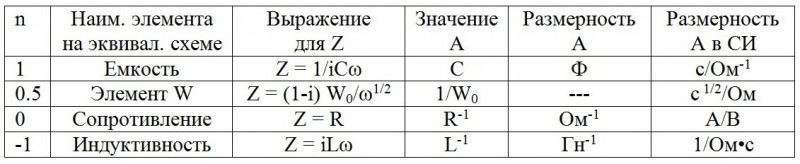 Для промежуточных значений n СРЕ описывает различный тип частотного распределения, аппроксимирующего поведение C, R, L и W с распределенными параметрами. При этом сами элементы СРЕ со значениями n, отличающимися от «стандартных» для C, R, L и W n=1, 0, -1, 0.5 уже не имеют ни ясного физического смысла, ни вменяемой размерности. Так, СРЕ с n немного меньшим, чем 1.00 – это как бы емкость, но довольно странная: через нее идет диффузионный поток частиц, интенсивность которого зависит от частоты (но не так просто, как в «обычном» RC-элементе, рассмотренном вначале — более сложным образом).
Для промежуточных значений n СРЕ описывает различный тип частотного распределения, аппроксимирующего поведение C, R, L и W с распределенными параметрами. При этом сами элементы СРЕ со значениями n, отличающимися от «стандартных» для C, R, L и W n=1, 0, -1, 0.5 уже не имеют ни ясного физического смысла, ни вменяемой размерности. Так, СРЕ с n немного меньшим, чем 1.00 – это как бы емкость, но довольно странная: через нее идет диффузионный поток частиц, интенсивность которого зависит от частоты (но не так просто, как в «обычном» RC-элементе, рассмотренном вначале — более сложным образом).
Если в рассмотренном выше RC участке цепи заменить С на СРЕ (n < 1.00),
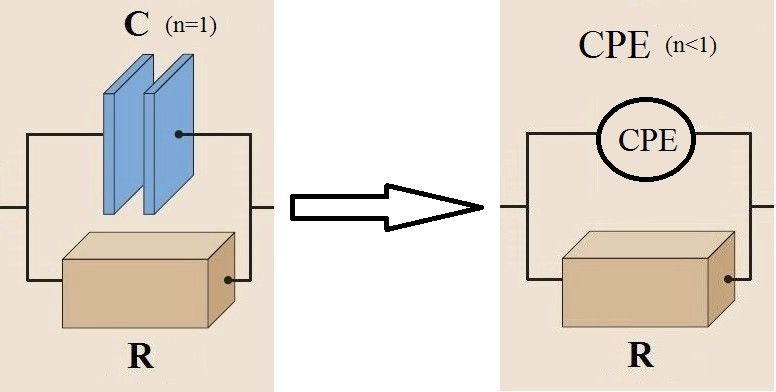 то в результате получается годограф, изображенный на рисунке
то в результате получается годограф, изображенный на рисунке
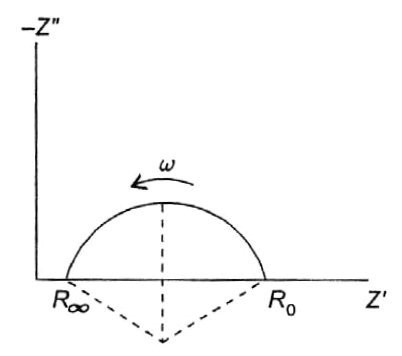 Это уже не полная полуокружность (см выше п.4.3.1), а некая ее часть. И чем больше n для CPE отличается от исходного значения n=1.00, тем эта часть меньше.
Это уже не полная полуокружность (см выше п.4.3.1), а некая ее часть. И чем больше n для CPE отличается от исходного значения n=1.00, тем эта часть меньше.
4.3.5. Апофеоз. Годограф реального аккумулятора Li-ion 18650
Вот рисунок из статьи, опубликованной в журнале «Электрохимия», 2008 г., №1
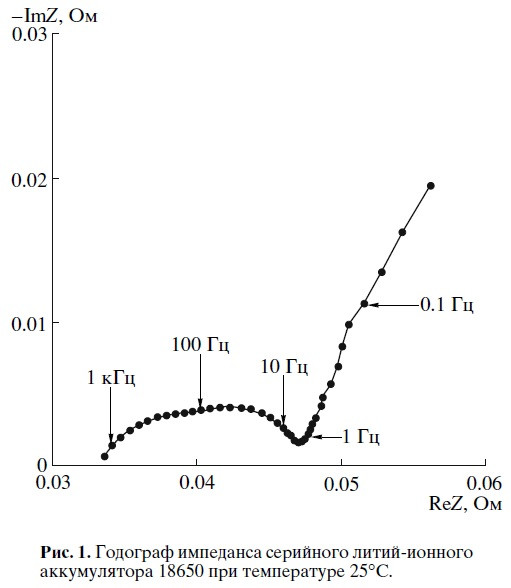 Полный текст статьи есть библиотечке, находящейся в облаке. На рисунке представлен годограф реального аккумулятора Li-ion 18650. Какой именно модели – осталось за кадром. В статье упомянуто, что «объектами измерений были коммерческие литий-ионные аккумуляторы производства фирм «Сони» и «Самсунг» типоразмера 18650, а так же лабораторные макеты в плоских корпусах из ламината». То, что на рисунке – это годограф одного из серийных образцов.
Полный текст статьи есть библиотечке, находящейся в облаке. На рисунке представлен годограф реального аккумулятора Li-ion 18650. Какой именно модели – осталось за кадром. В статье упомянуто, что «объектами измерений были коммерческие литий-ионные аккумуляторы производства фирм «Сони» и «Самсунг» типоразмера 18650, а так же лабораторные макеты в плоских корпусах из ламината». То, что на рисунке – это годограф одного из серийных образцов.
Обратите внимание, какое значение импеданса получено для частоты 1 кГц, фигурирующей в рекомендациях МЭК, международных стандартах и наших родных ГОСТах. Выполнено ли условие Z’’ = 0? Строго говоря – нет. Напомню, что выполнение условия Z’’ = 0 необходимо для того, чтобы сопротивление, измеренное на переменном токе, соответствовало омическому сопротивлению ХИТ R(a.c.) = R(о).
Если мысленно продолжить кривую годографа до пересечения с осью Z’, то в точке пересечения Z’ = 33 мОм. В тоже время, полный импеданс (то, что измеряется наYR1035) при 1 кГц по моим расчетам равен 35 мОм.
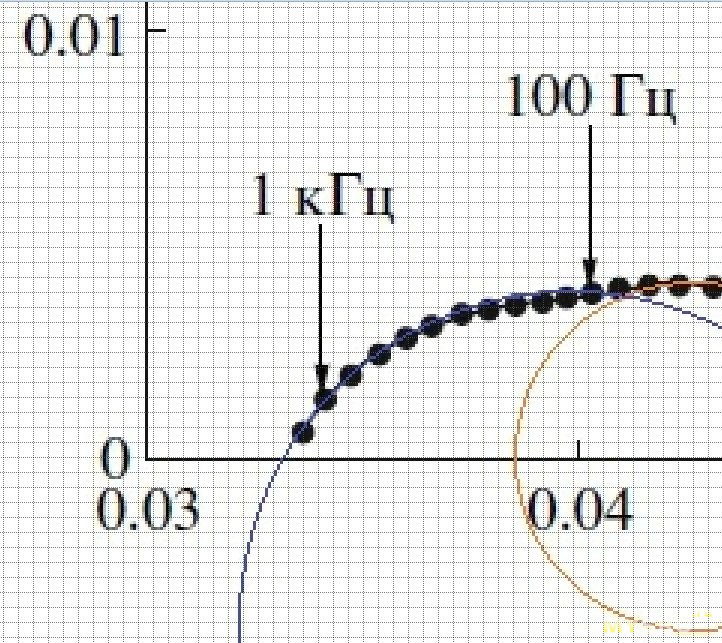 На самом деле, отличия между двумя этими значениями не так уж велики ~6%. Но кто даст гарантию, что так будет всегда, для любых аккумуляторов, батареек и их сборок?
На самом деле, отличия между двумя этими значениями не так уж велики ~6%. Но кто даст гарантию, что так будет всегда, для любых аккумуляторов, батареек и их сборок?
Да никто. Вот, к примеру, что можно почерпнуть из «EC-Lab — Application Note #59» (янв. 2017): исследование сборки из 120 элементов LiFeO4 в конфигурации 12S10P:
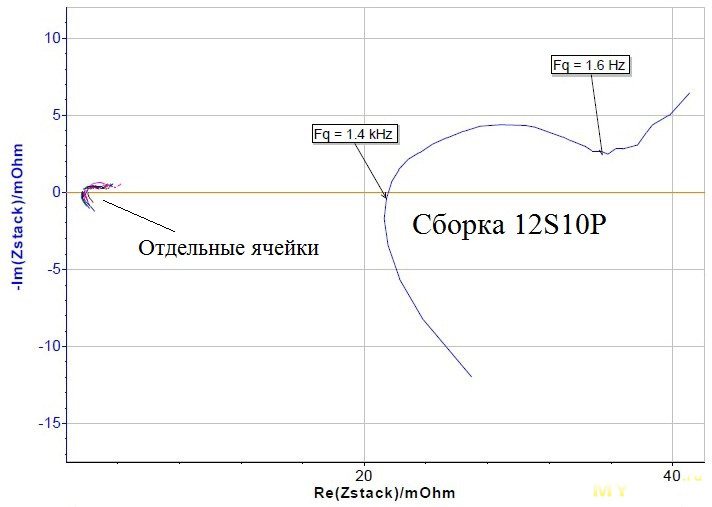
Или вот пример из Bio-Logic Tutorials. Part II – EC-Lab for battery testing ТЫЦ:
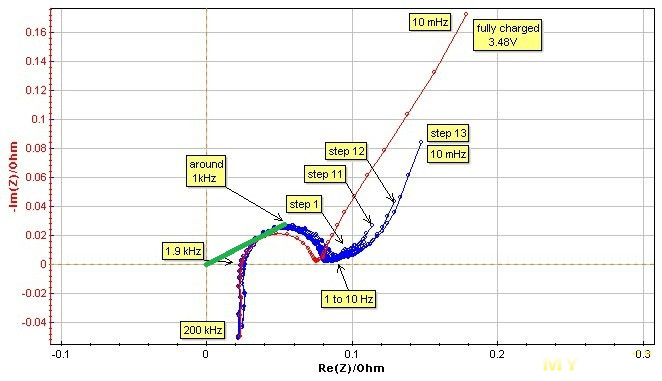 Показаны годографы некого литий-железо-фосфатного аккумулятора (3400 мАч) в процессе его разряда от 3.48 до 3.10 В. Разряжали в 13 этапов. После каждого этапа снимали годограф. Красная линия – исходное состояние, полностью заряженный гальванический элемент. ВСЕ кривые пересекают ось Z’ в районе 1.9 кГц при 21<Z’<24 мОм. Обратите внимание, где находится область 1 кГц. Полный импеданс |Z| (то, что измеряется на YR1035/1030):
Показаны годографы некого литий-железо-фосфатного аккумулятора (3400 мАч) в процессе его разряда от 3.48 до 3.10 В. Разряжали в 13 этапов. После каждого этапа снимали годограф. Красная линия – исходное состояние, полностью заряженный гальванический элемент. ВСЕ кривые пересекают ось Z’ в районе 1.9 кГц при 21<Z’<24 мОм. Обратите внимание, где находится область 1 кГц. Полный импеданс |Z| (то, что измеряется на YR1035/1030):
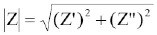 в области 1 кГц равен длине зеленой линии, |Z| ~40 мОм. Ошибка в определении R(o) ~ 90% в сторону завышения.
в области 1 кГц равен длине зеленой линии, |Z| ~40 мОм. Ошибка в определении R(o) ~ 90% в сторону завышения.
А вот годографы мелкого литий-ионного аккумулятора (даташит) в формфакторе «пуговки» 2032 с уровнем заряда 3.9 – 4.5В:
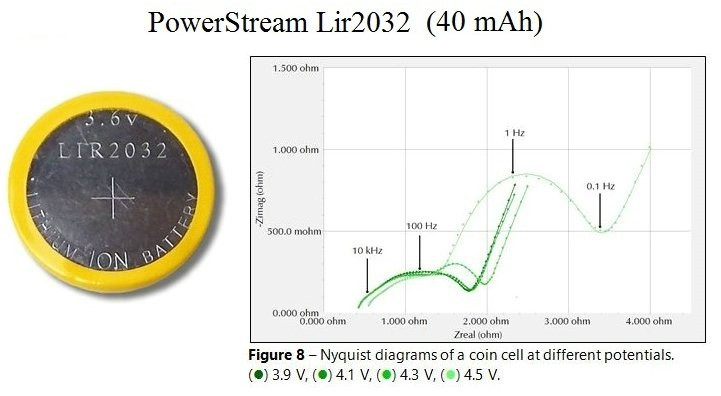 С какого перепуга тестировщики из Gamry перезаряжали малютку до 4.5В – неизвестно. Наверное, что бы картинка была поинтереснее. Ведь при «правильных» (ниже 4.2В) 3.9 и 4.1В годографы идентичны в пределах погрешности эксперимента. При 4.3В появляются явные изменения формы кривой. А при 4.5В не только кривая резко отличается, но и пересечение годографа с осью действительных значений наконец-то сдвигается. Что говорит о том, что омическое сопротивление (в отличии от поляризационного) – величина весьма консервативная.
С какого перепуга тестировщики из Gamry перезаряжали малютку до 4.5В – неизвестно. Наверное, что бы картинка была поинтереснее. Ведь при «правильных» (ниже 4.2В) 3.9 и 4.1В годографы идентичны в пределах погрешности эксперимента. При 4.3В появляются явные изменения формы кривой. А при 4.5В не только кривая резко отличается, но и пересечение годографа с осью действительных значений наконец-то сдвигается. Что говорит о том, что омическое сопротивление (в отличии от поляризационного) – величина весьма консервативная.
Но самое главное – это то, что условие Z’’ = 0 выполняется на частоте больше 10 кГц!
Отсюда 4 главных вывода по всему разделу в целом.
1) Измерение внутреннего сопротивления на частоте 1 кГц не дает никакой гарантии, что сопротивление, измеренное на частоте 1 кГц равно омическому сопротивлению элемента питания: R(1 кГц) = R(о).
2) С какой бы точностью ни был произведен замер R(1 кГц), его имеет смысл округлить как минимум до целых мОм. Практически всегда R(1 кГц) – это завышенная оценка значения R(о), в ряде случаев заметно завышенная. О проблеме корректного определения R(о) ниже будет еще пара слов. Даже не пара слов, а много слов и небольшой раздельчик.
3) В идеале нужно снимать годограф каждого элемента питания, но в домашних условиях это вряд ли достижимо.
4) Но все равно – замер на R(1 кГц) это все-таки лучше, чем ничего. Наверное.
4.3.6. Вместо заключения по разделу 4. Так чему же все-таки равно омическое сопротивление R(o)?
Наверное, у тех немногих, кто дошел-таки до чтения этого пункта, от такого вопроса может случиться истерика.
 Поверьте, мне очень жаль … но есть мнение, что определять омическое сопротивление таким образом, не совсем корректно. Краткий анализ ситуации неопределенности значения R(o) дан в информ. листке «EC-Lab — Application Note #62» (февр. 2017).
Поверьте, мне очень жаль … но есть мнение, что определять омическое сопротивление таким образом, не совсем корректно. Краткий анализ ситуации неопределенности значения R(o) дан в информ. листке «EC-Lab — Application Note #62» (февр. 2017).
Насколько я понимаю, суть в следующем.
Годограф любого ХИТ при неограниченном увеличении частоты имеет продолжение в области положительных значений мнимой части импеданса после прохождения точки Z’’= 0. Если это есть (а это есть практически всегда), то в эквивалентную схему вводится элемент типа индуктивности.
Выше уже приводился пример для трех аккумуляторов, что бы не мотать несколько страниц вверх, я приведу эту картинку еще раз:
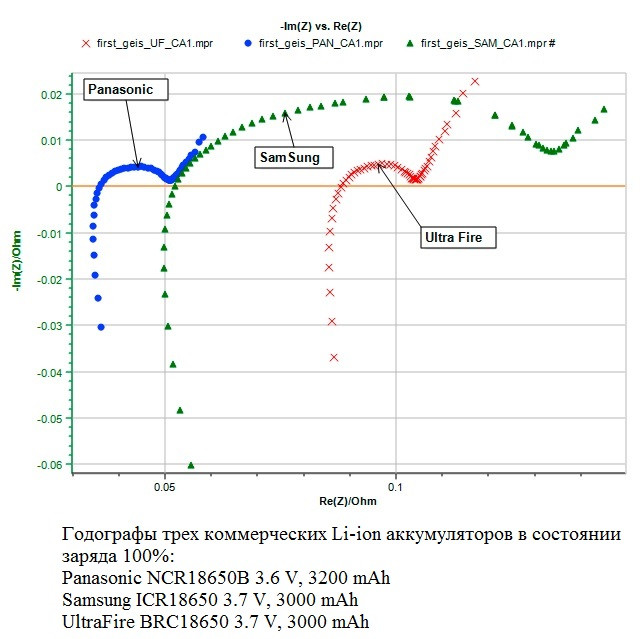 Напомню, что в электрохимии координаты Найквиста обычно выбираются таким образом, чтобы по оси ординат были отложены значения – Z’’, т.е. Z’’ с обратным знаком.
Напомню, что в электрохимии координаты Найквиста обычно выбираются таким образом, чтобы по оси ординат были отложены значения – Z’’, т.е. Z’’ с обратным знаком.
Еще напомню табличку, которая уже использовалась выше как пояснение сути «универсального элемента» эквивалентных схем – CPE.
 Годограф «чистой» индуктивности L (n=–1) – это луч, параллельный мнимой оси Z’’ (т.е. Z’=0), имеющий начало при Z’’=0. Понятно, что при сопряжении с дугой появляется некая переходная область:
Годограф «чистой» индуктивности L (n=–1) – это луч, параллельный мнимой оси Z’’ (т.е. Z’=0), имеющий начало при Z’’=0. Понятно, что при сопряжении с дугой появляется некая переходная область:
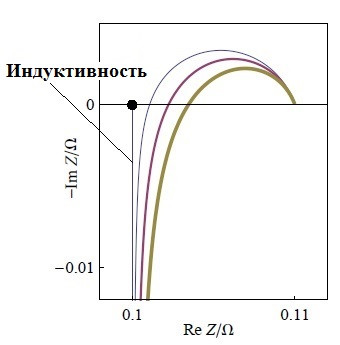 На этой картинке — чем толще кривая, тем больше значение некой индуктивности L, присутствующей в цепи. Обратите внимание, что при увеличении L точка пересечения годографа с осью Z’ смещается вправо.
На этой картинке — чем толще кривая, тем больше значение некой индуктивности L, присутствующей в цепи. Обратите внимание, что при увеличении L точка пересечения годографа с осью Z’ смещается вправо.
Высокочастотные «хвосты» индуктивностей на годографах, полученных экспериментально, почти всегда имеют наклон вправо (см. рисунки), поэтому на эквивалентных схемах они сопоставляются с элементами CPE (n> –1). По моему скромному разумению, если бы этих наклонов не было (а такое тоже бывает), то появление индуктивных составляющих на годографах можно было объяснить весьма банально. Подводящие провода + геометрия электродов (в цилиндрических элементах электроды закручены в спирали, в призматиках — в сильно сплющенные по бокам спирали). А вот эти самые наклоны разные группы исследователей трактует по-разному. И модно связывать с наличием SEI на обоих электродах. Статью на Гике (на днях Гик вернулся-таки на Хабр)писали переводили журналисты и там речь только об изолирующем слое на аноде. Сейчас вроде как доказано, что пассивирующие пленки SEI имеются не только на графитовом аноде, но и на катоде.
Но не суть.
Печалька в том, что я уже второй месяц мучительно пытаюсь понять каким боком слои SEI могут иметь отношение к паразитной индуктивности… Ну да ладно.
На рисунке ниже показан кусочек годографа Li-Ion ХИТ. Форма годографа и параметры элементов эквивалентной схемы разработчики компании BioLogic считают достаточно типичными для «обычных» литий-ионных ячеек аккумуляторов массового производства со всяко-разным составом катодов (за исключением LiFeO4).
Синяя точка (R1) на рисунке – это омическое сопротивление R(о), найденное расчетным путем (оптимизация параметров эквивалентной схемы по имеющимся экспериментальным данным):
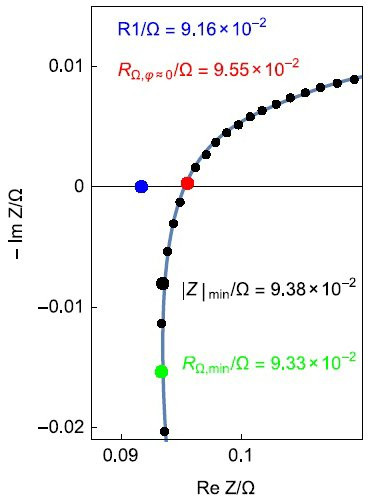 Далее: три оценки величины R(о) по трем характерным точкам на кривой:
Далее: три оценки величины R(о) по трем характерным точкам на кривой:
– красная точка – Z’’=0, пересечение годографа с осью Z’ (о чем говорилось в этом разделе многократно)
– черная точка – минимальное значение полного импеданса |Z|
– зеленая точка – соответствует минимальному значению Z’ на данном годографе.
Оценки R(о) по этим точкам отличаются от «правильного» значения R1 на 2-4% в сторону завышения искомой величины.
 Понятно, что это некий обобщенно-усредненный случай типа «средней температуры по больнице» или «сферического коня в вакууме». Для каждого конкретного экземпляра полностью заряженного ХИТ годограф будет в какой-то мере уникален в зависимости от «химии» катода, технологии производства и истории его эксплуатации. Но есть 2 общих момента:
Понятно, что это некий обобщенно-усредненный случай типа «средней температуры по больнице» или «сферического коня в вакууме». Для каждого конкретного экземпляра полностью заряженного ХИТ годограф будет в какой-то мере уникален в зависимости от «химии» катода, технологии производства и истории его эксплуатации. Но есть 2 общих момента:
1) оценка R(о) по любой точке годографа всегда [хотя бы немного] завышена;
2) в ряде случаев «процент завышения» будет больше 2-4%, полученных в данном примере.
Все это в полной мере относится и к «стрельбе с завязанными глазами» – изменениях на «ГОСТовской» частоте 1000 Гц. При этом ситуация усугубляется непредсказуемостью попадания в то или иное место неизвестной нам частотной кривой. Причем, «перелеты» относительно «зеленой точки» тоже приводят к дополнительной положительной ошибке в определении R(о). Хотя «недолеты» до «красной точки» будут усугублять эту самую ошибку еще сильнее.
5. Как правильно измерить внутреннее сопротивление ХИТ на постоянном токе R(d.c.)?
Если быть кратким, то никак.
Точнее, измерить-то можно. Разными способами и с использованием различных методик.
Разброс между результатами оценки R(d.c.) разными методами обычно составляет 10-15%. Иногда больше. А вот наиболее «правильного» метода измерения R(d.c.) человечество так не придумало.
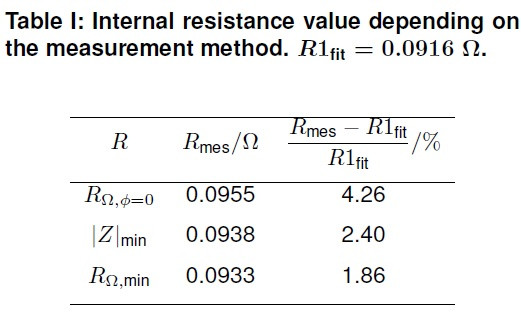
По этому вопросу очень рекомендую ознакомится с весьма интересной статьей (лежит в облаке под №19): H-G. Schweiger et al. Comparison of Several Methods for Determining the Internal Resistance of Lithium Ion Cells // Sensors, 2010. №10, р.5604-5625.
Там рассмотрены и применены следующие методы измерения R(d.c.) и R(a.c.):
 В качестве объекта исследования был выбран аккумулятор ENAX NX2P0M (2.0 Ah), годограф которого был показан в предыдущем разделе обзора.
В качестве объекта исследования был выбран аккумулятор ENAX NX2P0M (2.0 Ah), годограф которого был показан в предыдущем разделе обзора.
И вот что у них получилось:
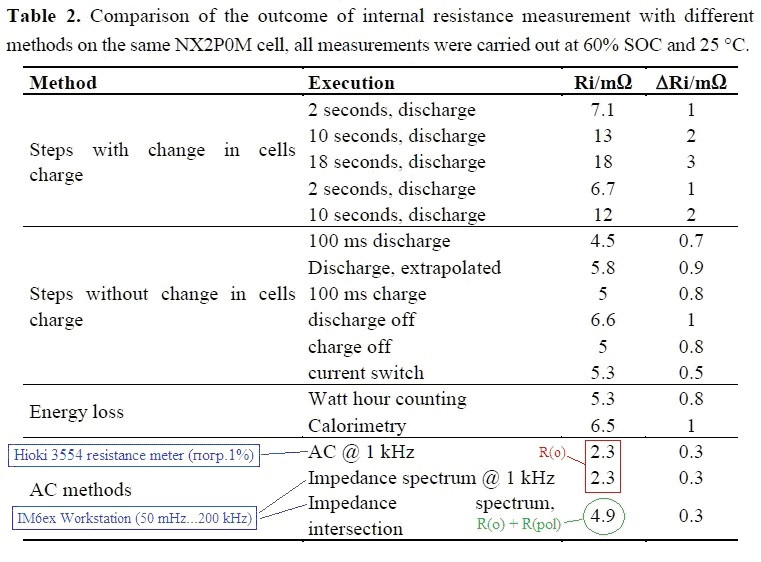 То же самое, но более наглядно (выдернул из другой статьи, где этот материал обсуждался):
То же самое, но более наглядно (выдернул из другой статьи, где этот материал обсуждался):
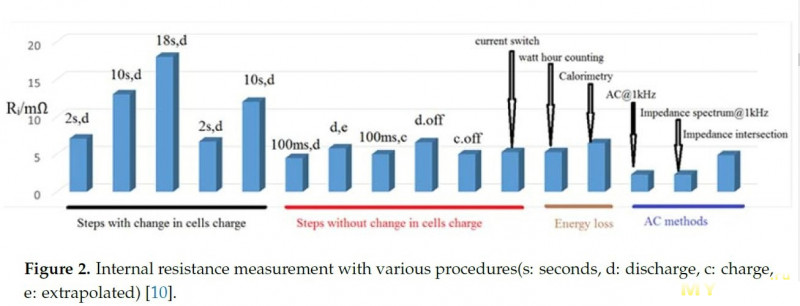 Немецкие ученые оказались людьми неленивыми и кроме обычных в этом деле электрофизических исследований сделали*** опыты с использованием калориметра (прямой замер количества теплоты, выделяющейся при прохождении тока).
Немецкие ученые оказались людьми неленивыми и кроме обычных в этом деле электрофизических исследований сделали*** опыты с использованием калориметра (прямой замер количества теплоты, выделяющейся при прохождении тока).
***Примечание. Скорее всего, они сами не делали. Заказали на стороне, отстегнули по гранту. Но это обычная практика комплексных и сильно разноплановых натурных испытаний последние 50-70 лет. Главное, что экспериментальная часть получилась более интересной.
Заключение по части II обзора. ЧТО ИМЕЕМ В СУХОМ ОСТАТКЕ
1) Что есть «внутреннее сопротивление» ХИТ?
Трудно сказать. В зависимости от того, какой смысл вкладывается в термин «внутреннее сопротивление».
2) Кроме того, «внутреннее сопротивление» (в разных ипостасях) может быть измерено (оценено) кучей способов. Разные способы дают разные результаты. Ни один из них не является единственно правильным.
3) Проблема в самом объекте исследования – ХИТ гальванического типа. К сожалению, по внутреннему устройству он несколько отличается от куска проволоки или резистора. Примерно так же, как микроскоп от гвоздя. И к тому же, ХИТ является источником эл. энергии. Заряженный конденсатор тоже является, но при его разряде-заряде не протекает куча химических и физических процессов. В той или иной мере взаимосвязанных.
Вот такие пирожки с котятами…
Спасибо всем, кто смог осилить то, что написано выше. И не по диагонали. И даже смог понять основные моменты вышеизложенного.
Disclaimer (отмазка): основной целью написания Части II являлось желание самому разобраться в том, что удалось накопать за несколько месяцев. Не уверен, что это следовало публиковать (тем паче на Муське), но угробить столько времени для «писанины в стол» тоже как то глупо. Если получилось слишком запутанно и громоздко — так и сам предмет рассмотрения один из наиболее мутных в электрохимии.
В начале приведен краткий список литературы. Первоисточники выложены в облако, искать не надо.
0. СЛОВАРИК аббревиатур и терминов
ХИТ — химический источник тока. Бывают гальванические и топливные. Далее речь идет только о гальванических ХИТ.
Импеданс (Z) – комплексное электрическое сопротивление Z=Z’+iZ’’.
Адмиттанс (А) – комплексная электропроводность, величина обратная импедансу. A=1/Z
ЭДС – «чисто химическая» разность потенциалов между электродами в гальваническом элементе, определяемая как разность электрохимических потенциалов анода и катода.
НРЦ — напряжение разорванной цепи, для одиночных элементов обычно примерно равно ЭДС.
Анод (химическое определение) – электрод, на котором происходит окисление.
Катод (химическое определение) – электрод, на котором происходит восстановление.
Электролит (химическое определение) – вещество, которое в растворе или расплаве (т.е. в жидкой среде) распадается на ионы (частично или полностью).
Электролит (техническое, НЕ химическое определение) – жидкая, твердая или гелеобразная среда, проводящая электрический ток за счет движения ионов. Ежели по-простому: электролит (техн.) = электролит (хим.) + растворитель.
ДЭС — двойной электрический слой. Всегда есть на границе раздела электрод/электролит.
ЛИТЕРАТУРА – все выложено в библиотечку НА ОБЛАКЕ
ОБЛАКО
А. По измерениям внутр. сопротивления и попыткам вытянуть из этого хоть какую-либо полезную информацию
01. [очень рекомендую ознакомиться с гл.1, там все очень просто]
Чупин Д.П. Параметрический метод контроля эксплуатационных характеристик аккумуляторных батарей. Дисс… уч. ст. к. т. н. Омск, 2014.
Читать – только гл.1 (Литобзор). Далее – очередное изобретение велосипеда…
02. Таганова А. А., Пак И.А. Герметичные химические источники тока для портативной аппаратуры: Справочник. СПб: Химиздат, 2003. 208 с.
Читать – гл.8 «Диагностика состояния химических источников тока»
03. [это лучше не читать, больше ошибок и опечаток, а нового ничего]
Таганова А. А., Бубнов Ю. И., Орлов С. Б. Герметичные химические источники тока: элементы и аккумуляторы, оборудование для испытаний и эксплуатации. СПб: Химиздат, 2005. 264 с.
04. Химические источники тока: Справочник / Под ред. Н. В. Коровина и А. М. Скундина. М.: Изд-во МЭИ. 2003. 740 с.
Читать – разд.1.8 «Методы физико-химических исследований ХИТ»
Б. По импедансной спектроскопии
05. [классика, три книжки ниже – это упрощенный и укороченный вариант книги Стойнова, методички для студентов]
Стойнов, 3.Б. Электрохимический импеданс / 3.Б. Стойнов, Б.М. Графов, Б.С. Савова-Стойнова, В. В. Елкин // М.: «Наука», 1991. 336 с.
06. [это самый краткий вариант]
07. [это вариант подлиннее]
Жуковский В.М., Бушкова О.В. Импедансная спектроскопия твердых электролитических материалов. Метод. пособие. Екатеринбург, 2000. 35 с.
08. [это еще более полный вариант: расширенный, углубленный и разжеванный]
Буянова Е.С., Емельянова Ю.В. Импедансная спектроскопия электролитических материалов. Метод. пособие. Екатеринбург, 2008. 70 с.
09. [можно пролистнуть как Мурзилку – много красивых картинок; в тексте я находил очепятки и явные ляпы… Внимание: весит ~100 Мб]
Springer Handbook of Electrochemical Energy
Наиболее интересный раздел: Pt.15. Lithium-Ion Batteries and Materials
В. Инф. листки от BioLogic (имп. спектроскопия)
10. EC-Lab — Application Note #8-Impedance, admittance, Nyquist, Bode, Black
11. EC-Lab — Application Note #21-Measurements of the double layer capacitance
12. EC-Lab — Application Note #23-EIS measurements on Li-ion batteries
13. EC-Lab — Application Note #38-A relation between AC and DC measurements
14. EC-Lab — Application Note #50-The simplicity of complex number and impedance diagrams
15. EC-Lab — Application Note #59-stack-LiFePO4(120 шт)
16. EC-Lab — Application Note #61-How to interpret lower frequencies impedance in batteries
17. EC-Lab — Application Note #62-How to measure the internal resistance of a battery using EIS
18. EC-Lab — White Paper #1-Studying batteries with Electrochemical Impedance Spectroscopy
Г. Сравнение методов измерения внутр. сопротивления
19. H-G. Schweiger et al. Comparison of Several Methods for Determining the Internal Resistance of Lithium Ion Cells // Sensors, 2010. №10, р.5604-5625.
Д. Обзоры (оба на английском) по SEI — защитных слоях на аноде и катоде в Li-Ion акк.
20. [краткий обзор]
21. [полный обзор]
Е. ГОСТы – куда же без них… В облаке не все, только те, что оказались под рукой.
ГОСТ Р МЭК 60285-2002 Аккумуляторы и батареи щелочные. Аккумуляторы никель-кадмиевые герметичные цилиндрические
ГОСТ Р МЭК 61951-1-2004 Аккумуляторы и аккумуляторные батареи, содержащие щелочной и другие некислотные электролиты. Портативные герметичные аккумуляторы. Часть 1. Никель-кадмий
ГОСТ Р МЭК 61951-2-2007 Аккумуляторы и аккумуляторные батареи, содержащие щелочной и другие некислотные электролиты. Портативные герметичные аккумуляторы. Часть 2. Никель-металл-гидрид
ГОСТ Р МЭК 61436-2004 Аккумуляторы и аккумуляторные батареи, содержащие щелочной и другие некислотные электролиты. Аккумуляторы никель-металлгидридные герметичные
ГОСТ Р МЭК 61960-2007 Аккумуляторы и аккумуляторные батареи, содержащие щелочной и другие некислотные электролиты. Аккумуляторы и аккумуляторные батареи литиевые для портативного применения
ГОСТ Р МЭК 896-1-95 Свинцово-кислотные стационарные батареи. Общие требования и методы испытаний. Часть 1. Открытые типы
ГОСТ Р МЭК 60896-2-99 Свинцово-кислотные стационарные батареи. Общие требования и методы испытаний. Часть 2. Закрытые типы
А. По измерениям внутр. сопротивления и попыткам вытянуть из этого хоть какую-либо полезную информацию
01. [очень рекомендую ознакомиться с гл.1, там все очень просто]
Чупин Д.П. Параметрический метод контроля эксплуатационных характеристик аккумуляторных батарей. Дисс… уч. ст. к. т. н. Омск, 2014.
Читать – только гл.1 (Литобзор). Далее – очередное изобретение велосипеда…
02. Таганова А. А., Пак И.А. Герметичные химические источники тока для портативной аппаратуры: Справочник. СПб: Химиздат, 2003. 208 с.
Читать – гл.8 «Диагностика состояния химических источников тока»
03. [это лучше не читать, больше ошибок и опечаток, а нового ничего]
Таганова А. А., Бубнов Ю. И., Орлов С. Б. Герметичные химические источники тока: элементы и аккумуляторы, оборудование для испытаний и эксплуатации. СПб: Химиздат, 2005. 264 с.
04. Химические источники тока: Справочник / Под ред. Н. В. Коровина и А. М. Скундина. М.: Изд-во МЭИ. 2003. 740 с.
Читать – разд.1.8 «Методы физико-химических исследований ХИТ»
Б. По импедансной спектроскопии
05. [классика, три книжки ниже – это упрощенный и укороченный вариант книги Стойнова, методички для студентов]
Стойнов, 3.Б. Электрохимический импеданс / 3.Б. Стойнов, Б.М. Графов, Б.С. Савова-Стойнова, В. В. Елкин // М.: «Наука», 1991. 336 с.
06. [это самый краткий вариант]
07. [это вариант подлиннее]
Жуковский В.М., Бушкова О.В. Импедансная спектроскопия твердых электролитических материалов. Метод. пособие. Екатеринбург, 2000. 35 с.
08. [это еще более полный вариант: расширенный, углубленный и разжеванный]
Буянова Е.С., Емельянова Ю.В. Импедансная спектроскопия электролитических материалов. Метод. пособие. Екатеринбург, 2008. 70 с.
09. [можно пролистнуть как Мурзилку – много красивых картинок; в тексте я находил очепятки и явные ляпы… Внимание: весит ~100 Мб]
Springer Handbook of Electrochemical Energy
Наиболее интересный раздел: Pt.15. Lithium-Ion Batteries and Materials
В. Инф. листки от BioLogic (имп. спектроскопия)
10. EC-Lab — Application Note #8-Impedance, admittance, Nyquist, Bode, Black
11. EC-Lab — Application Note #21-Measurements of the double layer capacitance
12. EC-Lab — Application Note #23-EIS measurements on Li-ion batteries
13. EC-Lab — Application Note #38-A relation between AC and DC measurements
14. EC-Lab — Application Note #50-The simplicity of complex number and impedance diagrams
15. EC-Lab — Application Note #59-stack-LiFePO4(120 шт)
16. EC-Lab — Application Note #61-How to interpret lower frequencies impedance in batteries
17. EC-Lab — Application Note #62-How to measure the internal resistance of a battery using EIS
18. EC-Lab — White Paper #1-Studying batteries with Electrochemical Impedance Spectroscopy
Г. Сравнение методов измерения внутр. сопротивления
19. H-G. Schweiger et al. Comparison of Several Methods for Determining the Internal Resistance of Lithium Ion Cells // Sensors, 2010. №10, р.5604-5625.
Д. Обзоры (оба на английском) по SEI — защитных слоях на аноде и катоде в Li-Ion акк.
20. [краткий обзор]
21. [полный обзор]
Е. ГОСТы – куда же без них… В облаке не все, только те, что оказались под рукой.
ГОСТ Р МЭК 60285-2002 Аккумуляторы и батареи щелочные. Аккумуляторы никель-кадмиевые герметичные цилиндрические
ГОСТ Р МЭК 61951-1-2004 Аккумуляторы и аккумуляторные батареи, содержащие щелочной и другие некислотные электролиты. Портативные герметичные аккумуляторы. Часть 1. Никель-кадмий
ГОСТ Р МЭК 61951-2-2007 Аккумуляторы и аккумуляторные батареи, содержащие щелочной и другие некислотные электролиты. Портативные герметичные аккумуляторы. Часть 2. Никель-металл-гидрид
ГОСТ Р МЭК 61436-2004 Аккумуляторы и аккумуляторные батареи, содержащие щелочной и другие некислотные электролиты. Аккумуляторы никель-металлгидридные герметичные
ГОСТ Р МЭК 61960-2007 Аккумуляторы и аккумуляторные батареи, содержащие щелочной и другие некислотные электролиты. Аккумуляторы и аккумуляторные батареи литиевые для портативного применения
ГОСТ Р МЭК 896-1-95 Свинцово-кислотные стационарные батареи. Общие требования и методы испытаний. Часть 1. Открытые типы
ГОСТ Р МЭК 60896-2-99 Свинцово-кислотные стационарные батареи. Общие требования и методы испытаний. Часть 2. Закрытые типы
4. Почему внутреннее сопротивление ХИТ на постоянном токе R(d.c.) и переменном токе R(a.c.) разные?
4.1. Вариант №1. Самое простое объяснение
Это даже не объяснение, а как бы констатация факта (взято у Тагановой).
1) То, что измеряется на постоянном токе R(d.c.) – это сумма двух сопротивлений: омического и поляризационного R(d.c.) = R(о) + R(pol).
2) А когда на переменном, да еще на «правильной» частоте 1 кГц, R(pol) исчезает и остается только R(о). То есть, R(1 кГц) = R(о).
По крайней мере, на это хочется надеяться экспертам МЭК, Алевтине Тагановой, а также многим (почти всем), кто измеряет R(d.c.) и R(1 кГц). И путем нехитрых арифметических действий получает R(о) и R(pol) по отдельности.
Если такое объяснение Вас устраивает, то дальше этот раздел можете не читать.
4.2. Вариант №2. Для особо интересующихся
Для начала попробуем схематически изобразить как выглядит богатый внутренний мир одной электрохимической ячейки. Возьмем, к примеру, гальванический элемент, где за перенос электричества во внутренней цепи отвечают ионы лития. Аккумулятор или батарейка – без разницы. На аккумуляторе может быть написано «Li-ion» или «Li-polimer» — по барабану.
 На картинке стрелочками изображено направление движения ионов Li(+) в процессе разряда (и саморазряда) элемента, т.е. когда элемент работает. Слева анод (окисление Li(0) – e(-) = Li(+)), справа катод (восстановление Li(+) + e(-) = Li(0)). Если поставить ХИТ на зарядку обозначения анод-катод поменяются местами. Но не суть.
На картинке стрелочками изображено направление движения ионов Li(+) в процессе разряда (и саморазряда) элемента, т.е. когда элемент работает. Слева анод (окисление Li(0) – e(-) = Li(+)), справа катод (восстановление Li(+) + e(-) = Li(0)). Если поставить ХИТ на зарядку обозначения анод-катод поменяются местами. Но не суть.Попробуем изобразить гальванический элемент в виде эквивалентной электрической цепи. Я тут набросал схемку. Все элементы этой схемы незримо присутствуют во всех ХИТ. Зачастую, весьма странно видоизменяясь. Но это сейчас не важно. Частности, нюансы, дополнительные усложнения пока опущены.
 или
илиR(A)+R(1)/C(1)+R(Э)+R(2)/C(2)+R(K)
Строка выше – это не арифметическое выражение. Это краткая запись структуры, изображенной на рисунке.
Основные составляющие этой схемы вроде как понятны. Кроме одного: что такое двойной электрический слой (ДЭС)?
Вообще говоря, ДЭС – штука довольно распространенная как в природе, так и в технике. Так как каждый из электродов гальванического элемента заряжен, то на его поверхности всегда есть слой «прилипших» противоионов (ионов со знаком заряда, обратным заряду электрода) из раствора электролита. Вот картинка из некой диссертации по морфологии почв. Только слова «глинистая частица» нужно заменить на «электрод»:
 Относительно слоев Штерна и Гуи можите не забивать себе голову – это Вам никогда не пригодится.
Относительно слоев Штерна и Гуи можите не забивать себе голову – это Вам никогда не пригодится.Про эти слои для сильно интересующихся. Но лучше не читать. Ничего интересного.
«Прилипшие» ионы – это т.н. слой Штерна. Ионы в нем считаются неподвижными, пока в системе не начинает протекать ток. Тогда они начинают двигаться перпендикулярно поверхности электрода. При разряде — в одном направлении, при заряде – в противоположном. Если речь идет об электрохимической ячейке, то на картинке выше изображен анод. В гальванических элементах на основе лития, прилипшие к электроду плюсики – это атомы лития, перешедшие в раствор в виде Li(+). При этом каждый из них оставил на аноде по одному электрону Li(0) – e(-) = Li(+). Минусики слева на рисунке – это и есть электроны, оставленные литием на аноде после ионизации. Ежели внешнюю цепь замкнуть, то избыточные электроны из слоя Штерна побегут по проводам через нагрузку к катоду, а освободившиеся от их притяжения ионы Li(+) начнут диффундировать в слой Гуи (вправо), при этом освобождая место для новых ионов лития, рождающихся из окисляющихся атомов лития Li(0) – e(-) = Li(+). На катоде все происходит в обратном порядке: катионы лития встречаются с электронами, пришедшими по внешней цепи и разряжаются до атомов Li(+) + e(-) = Li(0). Эти атомы встраиваются в вакансии (незанятые места) кристаллической решетки катода.
 Ионы в слое Штерна «голые», т.е. не окружены оболочкой молекул растворителя. Поэтому говорят: «ионы не сольватированы».
Ионы в слое Штерна «голые», т.е. не окружены оболочкой молекул растворителя. Поэтому говорят: «ионы не сольватированы».
Когда идет разряд, «голые» Li(+) переходят в слой Гуи и сольватируются, т.е. надевают шубу из молекул полярного растворителя. Сольватация*** – процесс завсегда энергетически выгодный, поэтому ионы это делают с удовольствием.
***Примечание: если в качестве растворителя выступает вода, то сольватация называется гидратацией. Раньше это проходили в школе.
Бонус для зашедших по спойлер: картинка из статьи, которая называется «КАЛЬКУЛЯТОР ГИДРАТАЦИИ». Просто посмотреть.
 Статья чисто женская. Поэтому смысла содержимого этого опуса я постичь не смог. Сюжет этой картинки в статье не объясняется. Такое впечатление, что красивая белая женщина наблюдает процесс гидратации ионов поваренной соли в водном растворе. И ей это нравится.
Статья чисто женская. Поэтому смысла содержимого этого опуса я постичь не смог. Сюжет этой картинки в статье не объясняется. Такое впечатление, что красивая белая женщина наблюдает процесс гидратации ионов поваренной соли в водном растворе. И ей это нравится.
 Ионы в слое Штерна «голые», т.е. не окружены оболочкой молекул растворителя. Поэтому говорят: «ионы не сольватированы».
Ионы в слое Штерна «голые», т.е. не окружены оболочкой молекул растворителя. Поэтому говорят: «ионы не сольватированы».Когда идет разряд, «голые» Li(+) переходят в слой Гуи и сольватируются, т.е. надевают шубу из молекул полярного растворителя. Сольватация*** – процесс завсегда энергетически выгодный, поэтому ионы это делают с удовольствием.
***Примечание: если в качестве растворителя выступает вода, то сольватация называется гидратацией. Раньше это проходили в школе.
Бонус для зашедших по спойлер: картинка из статьи, которая называется «КАЛЬКУЛЯТОР ГИДРАТАЦИИ». Просто посмотреть.
 Статья чисто женская. Поэтому смысла содержимого этого опуса я постичь не смог. Сюжет этой картинки в статье не объясняется. Такое впечатление, что красивая белая женщина наблюдает процесс гидратации ионов поваренной соли в водном растворе. И ей это нравится.
Статья чисто женская. Поэтому смысла содержимого этого опуса я постичь не смог. Сюжет этой картинки в статье не объясняется. Такое впечатление, что красивая белая женщина наблюдает процесс гидратации ионов поваренной соли в водном растворе. И ей это нравится.При прохождении тока, ДЭС ведет себя подобно конденсатору с очень большой утечкой. «Утечка» обусловлена протеканием окислительно-восстановительной реакции на границе раздела электрод-электролит. Все это можно представить в виде эквивалентной схемы, состоящей из идеального конденсатора С и идеального резистора R. Или, как говорят в нынешней электрохимии, «емкости и сопротивления с сосредоточенными параметрами».
 Как известно, для цепей, в которых протекает переменный ток, используется понятие импеданса. Импеданс (комплексное сопротивление) Z определяется как Z=Z’+iZ’’, где Z’ – активная (действительная), а Z” – реактивная (мнимая) составляющие полного импеданса. В координатах Re(Z) — Im(Z) все это выглядит следующим образом:
Как известно, для цепей, в которых протекает переменный ток, используется понятие импеданса. Импеданс (комплексное сопротивление) Z определяется как Z=Z’+iZ’’, где Z’ – активная (действительная), а Z” – реактивная (мнимая) составляющие полного импеданса. В координатах Re(Z) — Im(Z) все это выглядит следующим образом: Нетрудно заметить, что Z’ и Z’’ – это проекции импеданса на соответствующие оси.
Нетрудно заметить, что Z’ и Z’’ – это проекции импеданса на соответствующие оси.Для тех, кто пока не понимает, о чем идет речь – ЗДЕСЬ об этом рассказано предельно просто.
Общеизвестно, что для параллельно соединенных конденсатора и резистора активная и реактивная составляющие определяются выражениями:
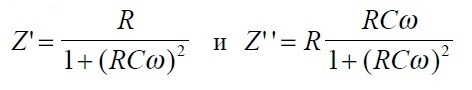 где ω — круговая частота.
где ω — круговая частота.Вывод

На практике проще всего сделать измерение активной части импеданса Z’.
В предельных случаях:
а) если частота = 0 (измерения на постоянном токе) то Z’ = R;
б) если частота стремится к бесконечности, то Z’ = 0.
Во втором случае конденсатор ведет себя по отношению к резистору как шунт с сопротивлением, равным нулю. В результате, сопротивление R уже никак не влияет на общее сопротивление цепи.
А что же будет получено между двумя крайними случаями?
Это лучше посмотреть на картинке. Графическая зависимость Z от частоты в координатах (Z’)/-(Z’’) (координаты Найквиста) называется годографом импеданса, или его спектром.
 Если на этом полукруге поставить точки через равные промежутки по частоте, то они будут расположены неравномерно, чем выше частота – тем гуще. То есть левая часть кривой стремится к Z’’ = 0 асимптотически.***
Если на этом полукруге поставить точки через равные промежутки по частоте, то они будут расположены неравномерно, чем выше частота – тем гуще. То есть левая часть кривой стремится к Z’’ = 0 асимптотически.******Примечание. Только в рамках данной примитивной модели. Годографы реальных литиевых ХИТ выглядят заметно сложнее. И нет там никакого асимптотического приближения. Спектральная кривая Z пресекает ось действительных значений Z и уходит в область положительных значений Z’’ (она внизу). Как пример – годограф некого японского литий-ионного аккумулятора ENAX (ENAX Inc., Tokyo, Japan) “High Power Cell” NX2P0M (2.0 Ah)
 Или вот пример из информационного листка «EC-Lab — Application Note #61» (янв. 2017) с более знакомыми нам испытуемыми:
Или вот пример из информационного листка «EC-Lab — Application Note #61» (янв. 2017) с более знакомыми нам испытуемыми: И еще пример для понимания частотных диапазонов из информ. листка «EC-Lab — Application Note #62» (февр. 2017) по измерению внутреннего сопротивления некого Li-ion АКБ:
И еще пример для понимания частотных диапазонов из информ. листка «EC-Lab — Application Note #62» (февр. 2017) по измерению внутреннего сопротивления некого Li-ion АКБ:
Теперь самое главное.
1) При измерениях внутреннего сопротивления на постоянном токе
R(d.c.) = R(о) + R(pol)
R(d.c.) = R(А) + R(Э) + R(К) + R(1) + R(2)
R(о) = R(А) + R(Э) + R(К)
R(pol) = R(1) + R(2).
2) Если для обоих электродов на частоте 1 кГц выполняется [примерно выполняется] условие Z’’ = 0, то
R(a.c.) = R(о)
R(a.c.) = R(А) + R(Э) + R(К).
Если такое объяснение Вас устраивает, то следующий пункт лучше не читать.
4.3. Продолжение. Для сильно-сильно интересующихся
1) Сами того не подозревая, мы залезли в местами интересный, но весьма заумный метод электрохимии, который называется спектроскопия электрохимического импеданса (СЭИ, EIS).
2) В настоящее время СЭИ считается наиболее мощным методом изучения электрохимических систем. Но, как говорится, есть «маленький нюанс»: однозначная интерпретация результатов в СЭИ – штука весьма затруднительная.
«Реальные электрохимические системы в общем случае являются многомерными, нелинейными, частично необратимыми, большими статистическими системами с распределенными параметрами в макро- и микро масштабе. В них протекают сложные процессы обмена энергии и массы, которые изменяют их параметры и структуры, вследствие чего они способны проявлять себя как нестационарные системы с памятью.» ©
Собственно об этом и будет в данной части изложения. Не так, чтобы сорвать покровы, раскрыть сокровенные тайны и расставить точки над «и». Нет, все намного скромнее – просто приподнять завесу, оценить обстановку в целом и больше туда не соваться…
Если все еще интересно, то продолжим.
RC-элемент был рассмотрен выше. Начинаем потихоньку усложнять модель и наблюдать за изменениями формы и положения годографа в системе координат Найквиста.
4.3.1. Добавляем сопротивление одного из электродов
 Тут все просто – годограф сдвигается вправо на величину R(A).
Тут все просто – годограф сдвигается вправо на величину R(A).
На самом деле, есть альтернативная эквивалентная схема, дающая такую же картинку. Но она от лукавого.

4.3.2. Добавляем электролит.
 Ну, понятно – годограф еще сдвинется вправо на величину R(Э).
Ну, понятно – годограф еще сдвинется вправо на величину R(Э).Все верно, сдвигается на R(Э). Но еще на годографе любого ХИТ появляется хвост в области сверхнизких частот (~1 Гц и меньше). Это так называемый диффузионный импеданс.
 Наличие на годографе хвоста в области очень низких частот было впервые объяснено Варбургом с использованием ряда упрощающих предположений. На самом деле, некоторые из них в реальных ячейках в принципе неосуществимы (например – диффузия из неограниченного объема). Тем не менее, до сих пор диффузионный хвост кривой годографа часто связывают (в нулевом приближении) с диффузионным импедансом Варбурга. Если кратко, то импеданс Варбурга описывается выражением
Наличие на годографе хвоста в области очень низких частот было впервые объяснено Варбургом с использованием ряда упрощающих предположений. На самом деле, некоторые из них в реальных ячейках в принципе неосуществимы (например – диффузия из неограниченного объема). Тем не менее, до сих пор диффузионный хвост кривой годографа часто связывают (в нулевом приближении) с диффузионным импедансом Варбурга. Если кратко, то импеданс Варбурга описывается выражением Слово «постоянная» для W(0) означает, что эта величина не зависит от частоты. Но зависит от кучи других факторов: концентрации, температуры и т.д. На самом деле, это не постоянная, а всего лишь коэффициент пропорциональности, не зависящий от одного параметра – частоты.
Слово «постоянная» для W(0) означает, что эта величина не зависит от частоты. Но зависит от кучи других факторов: концентрации, температуры и т.д. На самом деле, это не постоянная, а всего лишь коэффициент пропорциональности, не зависящий от одного параметра – частоты. Из уравнения выше следует, что Z’/Z’’=1. Поэтому в идеале годограф импеданса Варбурга выглядит очень просто:
 Это означает, что независимо от частоты, ток по фазе опережает напряжение на 45 град.
Это означает, что независимо от частоты, ток по фазе опережает напряжение на 45 град.Если наложить годограф Варбурга на годограф одного из электродов, то получится вот такая картинка:
 Для реальных электрохимических ячеек все это может выглядить несколько по-иному, но об этом будет ниже.
Для реальных электрохимических ячеек все это может выглядить несколько по-иному, но об этом будет ниже.И еще один момент – не надо пытаться экстраполировать импеданс Варбурга до частоты, равной 0. Потому что это бессмысленно. На постоянном токе никаких диффузионных импедансов не существует. Есть только омическое сопротивление электролита R(Э).
Про диффузионные импедансы. Несколько замечаний. Просто посмотреть
Как бы несколько существенных замечаний. Если Вы собираетесь писать диплом по СЭИ или типа того.
1) Кроме импеданса Варбурга (W), в методе СЭИ часто фигурирует импеданс Геришера (G). И то и другое — это элементы с сосредоточенными параметрами + диффузия должна быть из бесконечно удаленного источника бесконечной емкости (в смысле запаса ионов).
2) По теореме Эскобара: шо Варбурга, шо Геришера — рояли не играет, ибо ни то ни другое не наблюдалось на годогафах в чистом виде не может наблюдаться никогда и нигде.
Но часто наблюдается нечто местами похожее.
3) Проблема в двух моментах:
— диффузия частиц, переносящих заряд (т.е. создающих ток) она завсегда не из бесконечно удаленного источника (это очевидно — в любой батарейке расстояние между электродами конечно. И всего-то несколько миллиметров);
— внутри батарейки/аккумулятора отсутствуют элементы с сосредоточенными параметрами. Они там всегда распределенные.
Статья, где все это объясняется более-менее понятно для тех, кто в курсе про закон Фика.
4)Теперь — Главный момент. В реальных ХИТ диффузионные явления происходят не только в электролите или на внешней границе раздела электролит-электрод. Они еще идут внутри электродов. Точнее — их [электрохимически] активной части.
Посмотрите на картинку, которая уже была приведена выше:
 Тут и анод и катод — сложносоставные. Фольга из алюминия или меди — пассивная часть электрода. Она не принимает участия в электрохимических процессах. На фольгу нанесена активная часть. Благодаря которой эта штука и работает.
Тут и анод и катод — сложносоставные. Фольга из алюминия или меди — пассивная часть электрода. Она не принимает участия в электрохимических процессах. На фольгу нанесена активная часть. Благодаря которой эта штука и работает.
Ионы Li(+) перемещаются в пространстве (диффундируют, точнее — электродиффундируют) не только в объеме электролита, но и в активных частях электродов. В случае анода — это графит. В случае катода — это фазы переменного состава на основе оксидов лития и всяко-разных оксидов переходных металлов (кобальта, железа, никеля, марганца — им несть числа:)).
1) Кроме импеданса Варбурга (W), в методе СЭИ часто фигурирует импеданс Геришера (G). И то и другое — это элементы с сосредоточенными параметрами + диффузия должна быть из бесконечно удаленного источника бесконечной емкости (в смысле запаса ионов).
2) По теореме Эскобара: шо Варбурга, шо Геришера — рояли не играет, ибо ни то ни другое не наблюдалось на годогафах в чистом виде не может наблюдаться никогда и нигде.
Но часто наблюдается нечто местами похожее.
3) Проблема в двух моментах:
— диффузия частиц, переносящих заряд (т.е. создающих ток) она завсегда не из бесконечно удаленного источника (это очевидно — в любой батарейке расстояние между электродами конечно. И всего-то несколько миллиметров);
— внутри батарейки/аккумулятора отсутствуют элементы с сосредоточенными параметрами. Они там всегда распределенные.
Статья, где все это объясняется более-менее понятно для тех, кто в курсе про закон Фика.
4)Теперь — Главный момент. В реальных ХИТ диффузионные явления происходят не только в электролите или на внешней границе раздела электролит-электрод. Они еще идут внутри электродов. Точнее — их [электрохимически] активной части.
Посмотрите на картинку, которая уже была приведена выше:
 Тут и анод и катод — сложносоставные. Фольга из алюминия или меди — пассивная часть электрода. Она не принимает участия в электрохимических процессах. На фольгу нанесена активная часть. Благодаря которой эта штука и работает.
Тут и анод и катод — сложносоставные. Фольга из алюминия или меди — пассивная часть электрода. Она не принимает участия в электрохимических процессах. На фольгу нанесена активная часть. Благодаря которой эта штука и работает.Ионы Li(+) перемещаются в пространстве (диффундируют, точнее — электродиффундируют) не только в объеме электролита, но и в активных частях электродов. В случае анода — это графит. В случае катода — это фазы переменного состава на основе оксидов лития и всяко-разных оксидов переходных металлов (кобальта, железа, никеля, марганца — им несть числа:)).
4.3.3. Как учесть тот факт, что электродов два?
Да очень просто – полуокружности годографов 2-х электродов накладываются друг на друга:
 Примечание.На самом деле, годографы, изображенные выше, одинаково хорошо описывают ажник три разные эквивалентные схемы:
Примечание.На самом деле, годографы, изображенные выше, одинаково хорошо описывают ажник три разные эквивалентные схемы: Но сейчас это не важно. Или гляньте, что там под спойлером в п.4.3.1…
Но сейчас это не важно. Или гляньте, что там под спойлером в п.4.3.1…Ежели «по жизни» — левый годограф (две отдельные полуокружности) в случае реальных ХИТ никогда не наблюдается (лично я не встречал ни разу). А второй вариант — сплошь и рядом. Только это не полуокружности, а дуги (см ниже -«CPE»). Ну и радиусы у них могут быть разные (что вполне естественно). Бывают ситуации, когда две дуги сливаются в одну. Вот пример (выдернул из какого-то мануала по практическому применению метода СЭИ):
 Там 2 кривые: одна экспериментальная, вторая — расчетная по эквивалентной схеме в нижней части рисунка. Про то, откуда появляется индуктивность и про CPE-элемент, обозначенный как «Q», будет рассказано ниже.
Там 2 кривые: одна экспериментальная, вторая — расчетная по эквивалентной схеме в нижней части рисунка. Про то, откуда появляется индуктивность и про CPE-элемент, обозначенный как «Q», будет рассказано ниже.4.3.4. Что делать, если эксперимент не соответствует простейшим моделям?
В этом случае теоретики обычно говорят: «Тем хуже для эксперимента!». Шутка юмора.
Но на самом деле оказалось, что годографы реальных электрохимических ячеек не укладываются в ложе примитивных построений, изложенных выше. Причем всегда.
Экспериментаторы взвыли: «Дайте нам теоретическое объяснение!».
И теоретики дали почти универсальный ответ: элемент с постоянным сдвигом фазы (СРЕ – constant phase element). Его часто неправильно называют как «элемент постоянной фазы» — лобовой перевод с английского.
А потом добавили «контрольный в голову»: конечный элемент постоянного сдвига фазы (ВСР). И все вопросы с формальным описанием были закрыты. Но проблемы с объяснением многих моментов на уровне физики и химии процессов остались. Но не суть. Пусть с этим разбираются специалисты. Это их
Коротенько про СРЕ.
Все очень просто. Импеданс любого структурного элемента на эквивалентных схемах можно представить как частный случай вот такого выражения
 Для целых значений n=1, 0, -1 элемент СРЕ вырождается до классических элементов с сосредоточенными параметрами C, R, L. Для n=0.5 СРЕ дает импеданс Варбурга в чистом виде.
Для целых значений n=1, 0, -1 элемент СРЕ вырождается до классических элементов с сосредоточенными параметрами C, R, L. Для n=0.5 СРЕ дает импеданс Варбурга в чистом виде.  Для промежуточных значений n СРЕ описывает различный тип частотного распределения, аппроксимирующего поведение C, R, L и W с распределенными параметрами. При этом сами элементы СРЕ со значениями n, отличающимися от «стандартных» для C, R, L и W n=1, 0, -1, 0.5 уже не имеют ни ясного физического смысла, ни вменяемой размерности. Так, СРЕ с n немного меньшим, чем 1.00 – это как бы емкость, но довольно странная: через нее идет диффузионный поток частиц, интенсивность которого зависит от частоты (но не так просто, как в «обычном» RC-элементе, рассмотренном вначале — более сложным образом).
Для промежуточных значений n СРЕ описывает различный тип частотного распределения, аппроксимирующего поведение C, R, L и W с распределенными параметрами. При этом сами элементы СРЕ со значениями n, отличающимися от «стандартных» для C, R, L и W n=1, 0, -1, 0.5 уже не имеют ни ясного физического смысла, ни вменяемой размерности. Так, СРЕ с n немного меньшим, чем 1.00 – это как бы емкость, но довольно странная: через нее идет диффузионный поток частиц, интенсивность которого зависит от частоты (но не так просто, как в «обычном» RC-элементе, рассмотренном вначале — более сложным образом).Если в рассмотренном выше RC участке цепи заменить С на СРЕ (n < 1.00),
 то в результате получается годограф, изображенный на рисунке
то в результате получается годограф, изображенный на рисунке Это уже не полная полуокружность (см выше п.4.3.1), а некая ее часть. И чем больше n для CPE отличается от исходного значения n=1.00, тем эта часть меньше.
Это уже не полная полуокружность (см выше п.4.3.1), а некая ее часть. И чем больше n для CPE отличается от исходного значения n=1.00, тем эта часть меньше.4.3.5. Апофеоз. Годограф реального аккумулятора Li-ion 18650
Вот рисунок из статьи, опубликованной в журнале «Электрохимия», 2008 г., №1
 Полный текст статьи есть библиотечке, находящейся в облаке. На рисунке представлен годограф реального аккумулятора Li-ion 18650. Какой именно модели – осталось за кадром. В статье упомянуто, что «объектами измерений были коммерческие литий-ионные аккумуляторы производства фирм «Сони» и «Самсунг» типоразмера 18650, а так же лабораторные макеты в плоских корпусах из ламината». То, что на рисунке – это годограф одного из серийных образцов.
Полный текст статьи есть библиотечке, находящейся в облаке. На рисунке представлен годограф реального аккумулятора Li-ion 18650. Какой именно модели – осталось за кадром. В статье упомянуто, что «объектами измерений были коммерческие литий-ионные аккумуляторы производства фирм «Сони» и «Самсунг» типоразмера 18650, а так же лабораторные макеты в плоских корпусах из ламината». То, что на рисунке – это годограф одного из серийных образцов.Обратите внимание, какое значение импеданса получено для частоты 1 кГц, фигурирующей в рекомендациях МЭК, международных стандартах и наших родных ГОСТах. Выполнено ли условие Z’’ = 0? Строго говоря – нет. Напомню, что выполнение условия Z’’ = 0 необходимо для того, чтобы сопротивление, измеренное на переменном токе, соответствовало омическому сопротивлению ХИТ R(a.c.) = R(о).
Если мысленно продолжить кривую годографа до пересечения с осью Z’, то в точке пересечения Z’ = 33 мОм. В тоже время, полный импеданс (то, что измеряется наYR1035) при 1 кГц по моим расчетам равен 35 мОм.
 На самом деле, отличия между двумя этими значениями не так уж велики ~6%. Но кто даст гарантию, что так будет всегда, для любых аккумуляторов, батареек и их сборок?
На самом деле, отличия между двумя этими значениями не так уж велики ~6%. Но кто даст гарантию, что так будет всегда, для любых аккумуляторов, батареек и их сборок?Да никто. Вот, к примеру, что можно почерпнуть из «EC-Lab — Application Note #59» (янв. 2017): исследование сборки из 120 элементов LiFeO4 в конфигурации 12S10P:

Или вот пример из Bio-Logic Tutorials. Part II – EC-Lab for battery testing ТЫЦ:
 Показаны годографы некого литий-железо-фосфатного аккумулятора (3400 мАч) в процессе его разряда от 3.48 до 3.10 В. Разряжали в 13 этапов. После каждого этапа снимали годограф. Красная линия – исходное состояние, полностью заряженный гальванический элемент. ВСЕ кривые пересекают ось Z’ в районе 1.9 кГц при 21<Z’<24 мОм. Обратите внимание, где находится область 1 кГц. Полный импеданс |Z| (то, что измеряется на YR1035/1030):
Показаны годографы некого литий-железо-фосфатного аккумулятора (3400 мАч) в процессе его разряда от 3.48 до 3.10 В. Разряжали в 13 этапов. После каждого этапа снимали годограф. Красная линия – исходное состояние, полностью заряженный гальванический элемент. ВСЕ кривые пересекают ось Z’ в районе 1.9 кГц при 21<Z’<24 мОм. Обратите внимание, где находится область 1 кГц. Полный импеданс |Z| (то, что измеряется на YR1035/1030):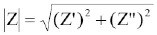 в области 1 кГц равен длине зеленой линии, |Z| ~40 мОм. Ошибка в определении R(o) ~ 90% в сторону завышения.
в области 1 кГц равен длине зеленой линии, |Z| ~40 мОм. Ошибка в определении R(o) ~ 90% в сторону завышения.А вот годографы мелкого литий-ионного аккумулятора (даташит) в формфакторе «пуговки» 2032 с уровнем заряда 3.9 – 4.5В:
 С какого перепуга тестировщики из Gamry перезаряжали малютку до 4.5В – неизвестно. Наверное, что бы картинка была поинтереснее. Ведь при «правильных» (ниже 4.2В) 3.9 и 4.1В годографы идентичны в пределах погрешности эксперимента. При 4.3В появляются явные изменения формы кривой. А при 4.5В не только кривая резко отличается, но и пересечение годографа с осью действительных значений наконец-то сдвигается. Что говорит о том, что омическое сопротивление (в отличии от поляризационного) – величина весьма консервативная.
С какого перепуга тестировщики из Gamry перезаряжали малютку до 4.5В – неизвестно. Наверное, что бы картинка была поинтереснее. Ведь при «правильных» (ниже 4.2В) 3.9 и 4.1В годографы идентичны в пределах погрешности эксперимента. При 4.3В появляются явные изменения формы кривой. А при 4.5В не только кривая резко отличается, но и пересечение годографа с осью действительных значений наконец-то сдвигается. Что говорит о том, что омическое сопротивление (в отличии от поляризационного) – величина весьма консервативная.Но самое главное – это то, что условие Z’’ = 0 выполняется на частоте больше 10 кГц!
Отсюда 4 главных вывода по всему разделу в целом.
1) Измерение внутреннего сопротивления на частоте 1 кГц не дает никакой гарантии, что сопротивление, измеренное на частоте 1 кГц равно омическому сопротивлению элемента питания: R(1 кГц) = R(о).
2) С какой бы точностью ни был произведен замер R(1 кГц), его имеет смысл округлить как минимум до целых мОм. Практически всегда R(1 кГц) – это завышенная оценка значения R(о), в ряде случаев заметно завышенная. О проблеме корректного определения R(о) ниже будет еще пара слов. Даже не пара слов, а много слов и небольшой раздельчик.
3) В идеале нужно снимать годограф каждого элемента питания, но в домашних условиях это вряд ли достижимо.
4) Но все равно – замер на R(1 кГц) это все-таки лучше, чем ничего. Наверное.
Просто посмотреть. Мой вариант расшифровки годографа аккумулятора Li-ion 18650 из статьи
Я использовал подходы из методик, предлагаемых в мануалах и информационных листках от производителей оборудования для СЭИ – BioLogic и Gamry. Точнее, сначала сам до них дошел, а потом оказалось, что это очевидно…;)
Определяемся с составными частями годографа: проводим одну прямую и две окружности:
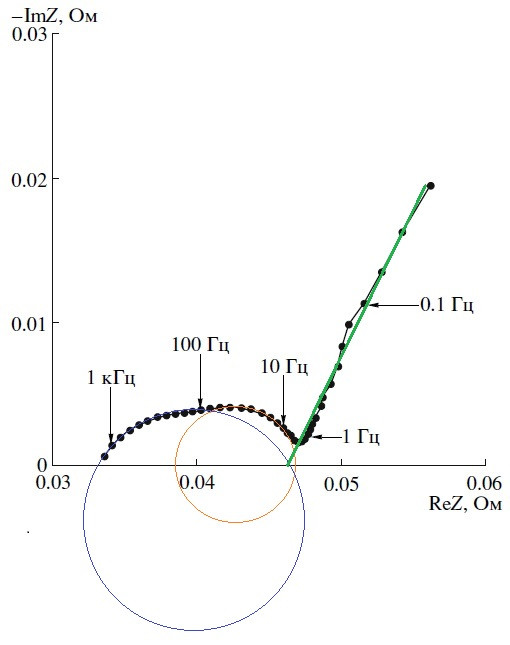 Делаем привязку частей годографа к составляющим банки 18650:
Делаем привязку частей годографа к составляющим банки 18650:
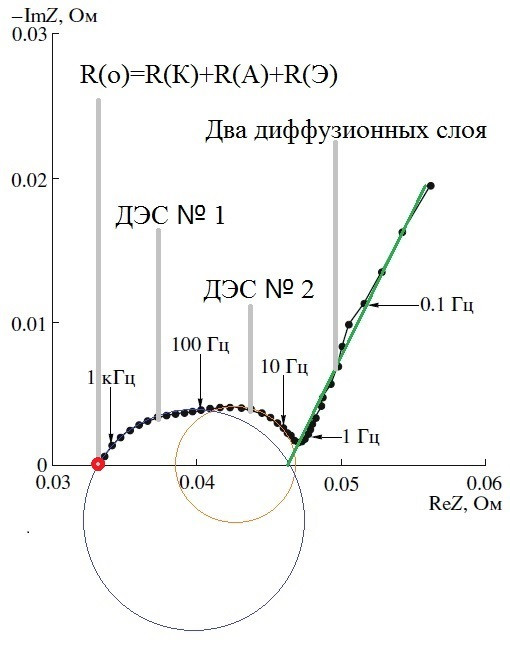 Следует учесть следующие моменты:
Следует учесть следующие моменты:
1) Прямая справа – это наложение годографов 2-х диффузионных элементов от 2-х электродов. Наклон прямой относительно оси абсцисс ~ 60 град., а не 45 (для «чистого» элемента Варбурга). Пусть это будет СРЕ(W) с n>0.5. В принципе, его можно разбросать на два электрода: СРЕ(W1) и СРЕ(W2). Но особого смысла в этом нет – в ходе расчетов численных параметров можно получить только интегральные оценки W(0) и n для СРЕ(W).
2) Малая дуга – это RC-элемент, соответствующий двойному электрическому слою у одного из электродов. Так как дуга примерно соответствует полуокружности, то емкость заменять на элемент СРЕ не нужно.
3) В вот вторая дуга – явно меньше полуокружности. Поэтому вместо RC-элемента напрашивается R-СРЕ(n<1).
4) Точка пересечения большой дуги с Z’ соответствует сумме всех омических сопротивлений в ХИТ, соединенных последовательно
R(о) = R(А) + R(Э) + R(К) + … + R(Х).
В рамках метода СЭИ разделение R(о) на составляющие невозможно.
Рисуем эквивалентную схему:
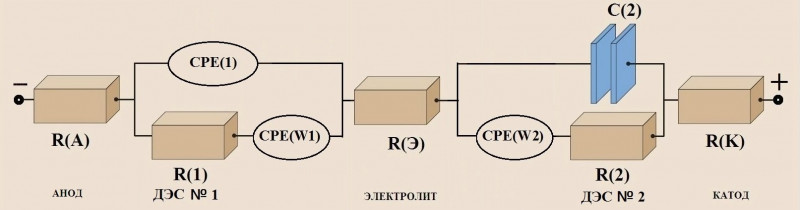 Далее запускается оптимизационная процедура подгонки параметров элементов таким образом, чтобы вычисленная кривая была максимально близка к годографу, полученному экспериментально.
Далее запускается оптимизационная процедура подгонки параметров элементов таким образом, чтобы вычисленная кривая была максимально близка к годографу, полученному экспериментально.
Но это уже другая история.
Определяемся с составными частями годографа: проводим одну прямую и две окружности:
 Делаем привязку частей годографа к составляющим банки 18650:
Делаем привязку частей годографа к составляющим банки 18650: Следует учесть следующие моменты:
Следует учесть следующие моменты:1) Прямая справа – это наложение годографов 2-х диффузионных элементов от 2-х электродов. Наклон прямой относительно оси абсцисс ~ 60 град., а не 45 (для «чистого» элемента Варбурга). Пусть это будет СРЕ(W) с n>0.5. В принципе, его можно разбросать на два электрода: СРЕ(W1) и СРЕ(W2). Но особого смысла в этом нет – в ходе расчетов численных параметров можно получить только интегральные оценки W(0) и n для СРЕ(W).
2) Малая дуга – это RC-элемент, соответствующий двойному электрическому слою у одного из электродов. Так как дуга примерно соответствует полуокружности, то емкость заменять на элемент СРЕ не нужно.
3) В вот вторая дуга – явно меньше полуокружности. Поэтому вместо RC-элемента напрашивается R-СРЕ(n<1).
4) Точка пересечения большой дуги с Z’ соответствует сумме всех омических сопротивлений в ХИТ, соединенных последовательно
R(о) = R(А) + R(Э) + R(К) + … + R(Х).
В рамках метода СЭИ разделение R(о) на составляющие невозможно.
Рисуем эквивалентную схему:
 Далее запускается оптимизационная процедура подгонки параметров элементов таким образом, чтобы вычисленная кривая была максимально близка к годографу, полученному экспериментально.
Далее запускается оптимизационная процедура подгонки параметров элементов таким образом, чтобы вычисленная кривая была максимально близка к годографу, полученному экспериментально. Но это уже другая история.
Просто посмотреть. А что же в результате получено авторами статьи?
Авторы статьи пошли значительно дальше. Что в общем-то и не удивительно для ученых-электрохимиков ИФХЭ РАН им. Фрумкина (ведущая организация в стране по методу СЭИ; академик А.Н. Фрумкин – один из основоположников СЭИ в мире). Они сделали лабораторные макеты Li-ion аккумуляторов, подобрали состав электролита и материал сепаратора. И изучили все это дело по 4-электродной схеме (2 анода+2 катода). В результате были получены кинетические и диффузионные параметры по отдельности для каждого электрода. Было показано, что и анод и катод можно представить в виде одной и той же эквивалентной схемы (но с разными параметрами):
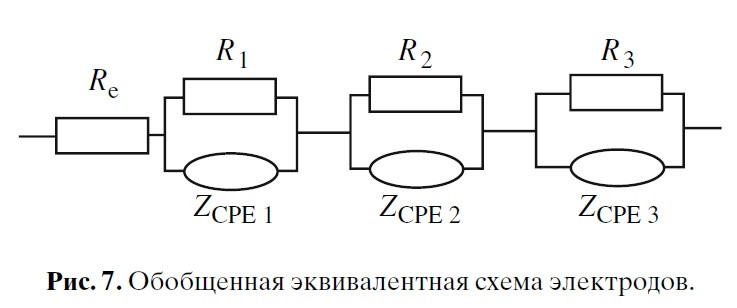 Ну и заключение, объясняющее эту схему:
Ну и заключение, объясняющее эту схему:
 В заключении упоминается пассивирующая пленка SEI – это важнейшая часть любой коммерческой литиевой ячейки. Можите погуглить. Есть неплохаястатья на Гиктаймс.
В заключении упоминается пассивирующая пленка SEI – это важнейшая часть любой коммерческой литиевой ячейки. Можите погуглить. Есть неплохаястатья на Гиктаймс.
 Ну и заключение, объясняющее эту схему:
Ну и заключение, объясняющее эту схему: В заключении упоминается пассивирующая пленка SEI – это важнейшая часть любой коммерческой литиевой ячейки. Можите погуглить. Есть неплохаястатья на Гиктаймс.
В заключении упоминается пассивирующая пленка SEI – это важнейшая часть любой коммерческой литиевой ячейки. Можите погуглить. Есть неплохаястатья на Гиктаймс.4.3.6. Вместо заключения по разделу 4. Так чему же все-таки равно омическое сопротивление R(o)?
Наверное, у тех немногих, кто дошел-таки до чтения этого пункта, от такого вопроса может случиться истерика.
 Поверьте, мне очень жаль … но есть мнение, что определять омическое сопротивление таким образом, не совсем корректно. Краткий анализ ситуации неопределенности значения R(o) дан в информ. листке «EC-Lab — Application Note #62» (февр. 2017).
Поверьте, мне очень жаль … но есть мнение, что определять омическое сопротивление таким образом, не совсем корректно. Краткий анализ ситуации неопределенности значения R(o) дан в информ. листке «EC-Lab — Application Note #62» (февр. 2017).Насколько я понимаю, суть в следующем.
Годограф любого ХИТ при неограниченном увеличении частоты имеет продолжение в области положительных значений мнимой части импеданса после прохождения точки Z’’= 0. Если это есть (а это есть практически всегда), то в эквивалентную схему вводится элемент типа индуктивности.
Выше уже приводился пример для трех аккумуляторов, что бы не мотать несколько страниц вверх, я приведу эту картинку еще раз:
 Напомню, что в электрохимии координаты Найквиста обычно выбираются таким образом, чтобы по оси ординат были отложены значения – Z’’, т.е. Z’’ с обратным знаком.
Напомню, что в электрохимии координаты Найквиста обычно выбираются таким образом, чтобы по оси ординат были отложены значения – Z’’, т.е. Z’’ с обратным знаком. Еще напомню табличку, которая уже использовалась выше как пояснение сути «универсального элемента» эквивалентных схем – CPE.
 Годограф «чистой» индуктивности L (n=–1) – это луч, параллельный мнимой оси Z’’ (т.е. Z’=0), имеющий начало при Z’’=0. Понятно, что при сопряжении с дугой появляется некая переходная область:
Годограф «чистой» индуктивности L (n=–1) – это луч, параллельный мнимой оси Z’’ (т.е. Z’=0), имеющий начало при Z’’=0. Понятно, что при сопряжении с дугой появляется некая переходная область:  На этой картинке — чем толще кривая, тем больше значение некой индуктивности L, присутствующей в цепи. Обратите внимание, что при увеличении L точка пересечения годографа с осью Z’ смещается вправо.
На этой картинке — чем толще кривая, тем больше значение некой индуктивности L, присутствующей в цепи. Обратите внимание, что при увеличении L точка пересечения годографа с осью Z’ смещается вправо. Высокочастотные «хвосты» индуктивностей на годографах, полученных экспериментально, почти всегда имеют наклон вправо (см. рисунки), поэтому на эквивалентных схемах они сопоставляются с элементами CPE (n> –1). По моему скромному разумению, если бы этих наклонов не было (а такое тоже бывает), то появление индуктивных составляющих на годографах можно было объяснить весьма банально. Подводящие провода + геометрия электродов (в цилиндрических элементах электроды закручены в спирали, в призматиках — в сильно сплющенные по бокам спирали). А вот эти самые наклоны разные группы исследователей трактует по-разному. И модно связывать с наличием SEI на обоих электродах. Статью на Гике (на днях Гик вернулся-таки на Хабр)
Но не суть.
Печалька в том, что я уже второй месяц мучительно пытаюсь понять каким боком слои SEI могут иметь отношение к паразитной индуктивности… Ну да ладно.
На рисунке ниже показан кусочек годографа Li-Ion ХИТ. Форма годографа и параметры элементов эквивалентной схемы разработчики компании BioLogic считают достаточно типичными для «обычных» литий-ионных ячеек аккумуляторов массового производства со всяко-разным составом катодов (за исключением LiFeO4).
Синяя точка (R1) на рисунке – это омическое сопротивление R(о), найденное расчетным путем (оптимизация параметров эквивалентной схемы по имеющимся экспериментальным данным):
 Далее: три оценки величины R(о) по трем характерным точкам на кривой:
Далее: три оценки величины R(о) по трем характерным точкам на кривой:– красная точка – Z’’=0, пересечение годографа с осью Z’ (о чем говорилось в этом разделе многократно)
– черная точка – минимальное значение полного импеданса |Z|
– зеленая точка – соответствует минимальному значению Z’ на данном годографе.
Оценки R(о) по этим точкам отличаются от «правильного» значения R1 на 2-4% в сторону завышения искомой величины.
 Понятно, что это некий обобщенно-усредненный случай типа «средней температуры по больнице» или «сферического коня в вакууме». Для каждого конкретного экземпляра полностью заряженного ХИТ годограф будет в какой-то мере уникален в зависимости от «химии» катода, технологии производства и истории его эксплуатации. Но есть 2 общих момента:
Понятно, что это некий обобщенно-усредненный случай типа «средней температуры по больнице» или «сферического коня в вакууме». Для каждого конкретного экземпляра полностью заряженного ХИТ годограф будет в какой-то мере уникален в зависимости от «химии» катода, технологии производства и истории его эксплуатации. Но есть 2 общих момента:1) оценка R(о) по любой точке годографа всегда [хотя бы немного] завышена;
2) в ряде случаев «процент завышения» будет больше 2-4%, полученных в данном примере.
Все это в полной мере относится и к «стрельбе с завязанными глазами» – изменениях на «ГОСТовской» частоте 1000 Гц. При этом ситуация усугубляется непредсказуемостью попадания в то или иное место неизвестной нам частотной кривой. Причем, «перелеты» относительно «зеленой точки» тоже приводят к дополнительной положительной ошибке в определении R(о). Хотя «недолеты» до «красной точки» будут усугублять эту самую ошибку еще сильнее.
5. Как правильно измерить внутреннее сопротивление ХИТ на постоянном токе R(d.c.)?
Если быть кратким, то никак.
Точнее, измерить-то можно. Разными способами и с использованием различных методик.
Разброс между результатами оценки R(d.c.) разными методами обычно составляет 10-15%. Иногда больше. А вот наиболее «правильного» метода измерения R(d.c.) человечество так не придумало.
По этому вопросу очень рекомендую ознакомится с весьма интересной статьей (лежит в облаке под №19): H-G. Schweiger et al. Comparison of Several Methods for Determining the Internal Resistance of Lithium Ion Cells // Sensors, 2010. №10, р.5604-5625.
Там рассмотрены и применены следующие методы измерения R(d.c.) и R(a.c.):
 В качестве объекта исследования был выбран аккумулятор ENAX NX2P0M (2.0 Ah), годограф которого был показан в предыдущем разделе обзора.
В качестве объекта исследования был выбран аккумулятор ENAX NX2P0M (2.0 Ah), годограф которого был показан в предыдущем разделе обзора.И вот что у них получилось:
 То же самое, но более наглядно (выдернул из другой статьи, где этот материал обсуждался):
То же самое, но более наглядно (выдернул из другой статьи, где этот материал обсуждался): Немецкие ученые оказались людьми неленивыми и кроме обычных в этом деле электрофизических исследований сделали*** опыты с использованием калориметра (прямой замер количества теплоты, выделяющейся при прохождении тока).
Немецкие ученые оказались людьми неленивыми и кроме обычных в этом деле электрофизических исследований сделали*** опыты с использованием калориметра (прямой замер количества теплоты, выделяющейся при прохождении тока).***Примечание. Скорее всего, они сами не делали. Заказали на стороне, отстегнули по гранту. Но это обычная практика комплексных и сильно разноплановых натурных испытаний последние 50-70 лет. Главное, что экспериментальная часть получилась более интересной.
Кой-какие замечания. Читать не обязательно
Особый интерес у меня вызвала нижняя часть таблички: «AC methods». Там представлены результаты измерений на японском тестере Hioki 3554 на частоте 1 кГц и на некой немецкой установке для СЭИ – IM6ex Workstation.
То, что выделено в таблице красным – это оценка «чисто» омического сопротивления на частоте 1 кГц. Не удивительно, что показания двух приборов совпадают.
Кроме годографа в системе координат Найквиста, в статье представлены графики в системе Боде. В СЭИ диаграммы Боде и Найквиста используются одинаково часто, так как это 2 взаимодополняющих способа графического отображения результатов спектрального исследования импеданса. На диаграмме Боде всегда присутствуют 2 кривые:
— зависимость полного импеданса системы от частоты (обычно – логарифма частоты);
— зависимость сдвига по фазе [тестового сигнала после прохождения через исследуемый объект] от частоты (логарифма частоты).
Вот рисунок из статьи:
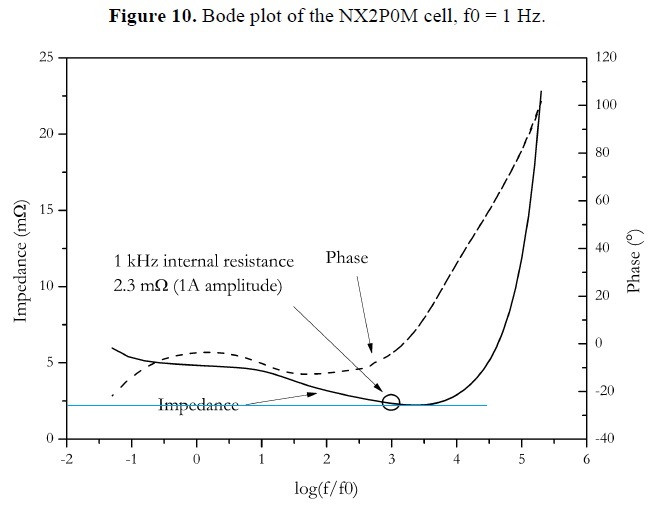 Черным кружком отмечено значение Z на «правильной» частоте 1 кГц.
Черным кружком отмечено значение Z на «правильной» частоте 1 кГц.
Синюю линию провел я – это минимальное значение модуля полного импеданса |Z|. На крайнем графике предыдущего раздела это жирная черная точка. В принципе, оценки (на 1 кГц и по минимуму импеданса) почти совпадают, что не может не радовать.
А вот как они определили общее сопротивление (в таблице отмечено зеленым) – тут есть путаница. Авторы говорят, что «на годографе Найквиста значение 4.9 мОм – это действительная часть импеданса, соответствующего пересечению полукруга и прямой Варбурга». Ну, во-первых, там нет полукруга, есть его часть (элемент CPE), которую лучше назвать дугой. Да и та там представлена в неявном виде. Во-вторых, определять общее сопротивление таким образом – плохая идея (см. методички для студентов в облаке). Общему сопротивлению соответствует другое пересечение: вышеозначенной дуги и оси действительных значений Z’. Я сделал простенькое построение по ихним данным:
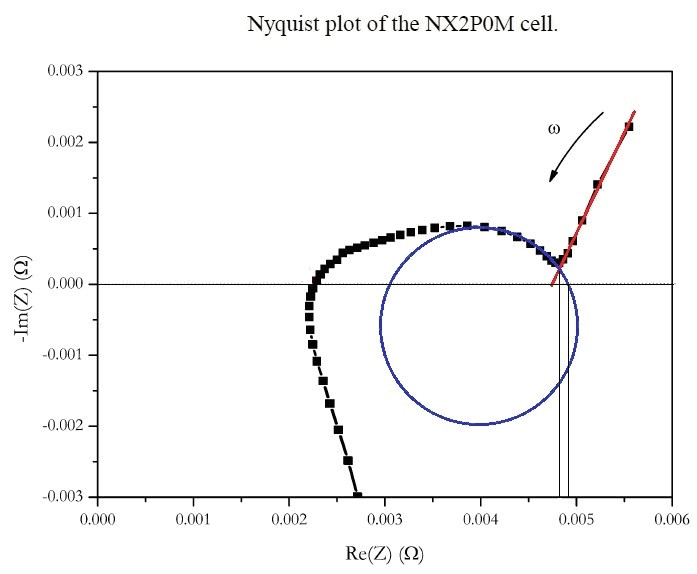 Левый перпендикуляр – это то, что заявляют авторы статьи. Забавно, но при этом получается R= 4.8 мОм. А вот если сделать так, как пишут во всех учебниках по СЭИ и использовать значение сопротивления, отсекаемое правым перпендикуляром, то получим R= 4.9 мОм. У меня есть предположение по этому поводу… Точнее — я, скорее всего, знаю, почему авторы не в зуб ногой в этом вопросе. Но не суть.
Левый перпендикуляр – это то, что заявляют авторы статьи. Забавно, но при этом получается R= 4.8 мОм. А вот если сделать так, как пишут во всех учебниках по СЭИ и использовать значение сопротивления, отсекаемое правым перпендикуляром, то получим R= 4.9 мОм. У меня есть предположение по этому поводу… Точнее — я, скорее всего, знаю, почему авторы не в зуб ногой в этом вопросе. Но не суть.
Не смотря ни на что, статья и интересная и полезная (ИМХО).
То, что выделено в таблице красным – это оценка «чисто» омического сопротивления на частоте 1 кГц. Не удивительно, что показания двух приборов совпадают.
Кроме годографа в системе координат Найквиста, в статье представлены графики в системе Боде. В СЭИ диаграммы Боде и Найквиста используются одинаково часто, так как это 2 взаимодополняющих способа графического отображения результатов спектрального исследования импеданса. На диаграмме Боде всегда присутствуют 2 кривые:
— зависимость полного импеданса системы от частоты (обычно – логарифма частоты);
— зависимость сдвига по фазе [тестового сигнала после прохождения через исследуемый объект] от частоты (логарифма частоты).
Вот рисунок из статьи:
 Черным кружком отмечено значение Z на «правильной» частоте 1 кГц.
Черным кружком отмечено значение Z на «правильной» частоте 1 кГц.Синюю линию провел я – это минимальное значение модуля полного импеданса |Z|. На крайнем графике предыдущего раздела это жирная черная точка. В принципе, оценки (на 1 кГц и по минимуму импеданса) почти совпадают, что не может не радовать.
А вот как они определили общее сопротивление (в таблице отмечено зеленым) – тут есть путаница. Авторы говорят, что «на годографе Найквиста значение 4.9 мОм – это действительная часть импеданса, соответствующего пересечению полукруга и прямой Варбурга». Ну, во-первых, там нет полукруга, есть его часть (элемент CPE), которую лучше назвать дугой. Да и та там представлена в неявном виде. Во-вторых, определять общее сопротивление таким образом – плохая идея (см. методички для студентов в облаке). Общему сопротивлению соответствует другое пересечение: вышеозначенной дуги и оси действительных значений Z’. Я сделал простенькое построение по ихним данным:
 Левый перпендикуляр – это то, что заявляют авторы статьи. Забавно, но при этом получается R= 4.8 мОм. А вот если сделать так, как пишут во всех учебниках по СЭИ и использовать значение сопротивления, отсекаемое правым перпендикуляром, то получим R= 4.9 мОм. У меня есть предположение по этому поводу… Точнее — я, скорее всего, знаю, почему авторы не в зуб ногой в этом вопросе. Но не суть.
Левый перпендикуляр – это то, что заявляют авторы статьи. Забавно, но при этом получается R= 4.8 мОм. А вот если сделать так, как пишут во всех учебниках по СЭИ и использовать значение сопротивления, отсекаемое правым перпендикуляром, то получим R= 4.9 мОм. У меня есть предположение по этому поводу… Точнее — я, скорее всего, знаю, почему авторы не в зуб ногой в этом вопросе. Но не суть. Не смотря ни на что, статья и интересная и полезная (ИМХО).
Заключение по части II обзора. ЧТО ИМЕЕМ В СУХОМ ОСТАТКЕ
1) Что есть «внутреннее сопротивление» ХИТ?
Трудно сказать. В зависимости от того, какой смысл вкладывается в термин «внутреннее сопротивление».
2) Кроме того, «внутреннее сопротивление» (в разных ипостасях) может быть измерено (оценено) кучей способов. Разные способы дают разные результаты. Ни один из них не является единственно правильным.
3) Проблема в самом объекте исследования – ХИТ гальванического типа. К сожалению, по внутреннему устройству он несколько отличается от куска проволоки или резистора. Примерно так же, как микроскоп от гвоздя. И к тому же, ХИТ является источником эл. энергии. Заряженный конденсатор тоже является, но при его разряде-заряде не протекает куча химических и физических процессов. В той или иной мере взаимосвязанных.
Вот такие пирожки с котятами…
Спасибо всем, кто смог осилить то, что написано выше. И не по диагонали. И даже смог понять основные моменты вышеизложенного.
Самые обсуждаемые обзоры
| +70 |
4339
213
|
| +83 |
4136
150
|
| +181 |
3890
231
|
| +64 |
3841
85
|
| +86 |
4294
94
|
проще и конкретнее для простолюдинов, как я. Я о том, что графики измерений показывают отличия.
И можно и нужно.
Все в строгом в соответствии с рекомендациями МЭК и ГОСТами.
Я просто хотел показать, насколько то, что «полагается» измерять соответствует тому, чего хочет пользователь от устройств такого рода.
Типа: ожидание-реальность.;)
А по-хорошему — надо годографы снимать…
Может, самодельщики придумают КАК?
Низкий поклон им тогда и карму бесконечную.
Казалось бы — можно и без нее. Просто вычитать то, что получается, ежели закоротить.
Ан нет — может появиться дополнительная погрешность. На малых сопротивлениях — несколько десятых мОм.
а так хотелось сечение померять, зная длину…
если провод тонкий, еще скин-эффект может вылезти. В 1 части я приводил табличку…
Не, ну правда. Если эти аккумуляторы мы используем для питания какой-то аппаратуры, т.е. ток в цепи аккумулятора постоянный, и нам как правило нужно знать, потянет ли этот аккумулятор такую нагрузку (т.е. при таком токе потребления обеспечит ли аккумулятор нужное напряжение), то нафига, спрашивается, нам измерять его сопротивление на частоте 1 кГц, если работать он будет на постоянном токе?
Про обзоры (не здесь, а в научной и научно-популярной литературе) что-нибудь слышали?
Вполне возможно.
Это научно-популярная мурзилка. Для людей, далеких от данной тематики.
Подобных в Рунете я не встречал. Потому и выложил — может кому-то окажется полезной.
Что будет дальше поглядим.
В тексте закодирован приз самому внимательному читателю.
Кто прочтет две части обзора и соберет ключевые слова — получит приз самому ?%*%*? читателю месяца :)
Как верно отметил автор, модель батареи должна соответствовать ее реальной сущности. К сожалению, он не довел эту мысль дальше, до вполне полезного вывода — полезной информацией о внутреннем сопротивлении банки является только ее активное (резистивное) сопротивление. Комплексные, реактивные (импеданс) — всё это интересно, но практического применения не имеет.
Повторюсь, практического применения. Это внутреннее сопротивление (скажем проще — ESR) влияет на нагрев батареи при выполнении зарядно/разрядных режимов. Реактивные элементы на нагрев не влияют, а потому к «тепловой» характеристике не относятся. Увеличенная емкостная составляющая никакого вреда не приносит, а индуктивная — да, вред есть, но не забывайте о подключении батареи к устройству (и сопряженную с этим индуктивность проводов) и обязательном наличии на устройстве блокировочных конденсаторов.
Кстати, об индуктивности. В sudj говорят об импедансе и быстро умывают руки от того, что сказали. А теперь о конкретных значениях. Понятно, что сие зависит от конструкции банки и батареи в целом… но, эта самая индуктивность измеряется в единицах-десятках nH. Фактически, такую-же индуктивность имеет провод схожей длины. Интересно, почему-бы это?…
Короткий вывод — в ГОСТ'е измеряют полное сопротивление, что есть чушь. Но, на то он и ГОСТ, дабы проводить измерения с помощью [] и палок (поверенных). Не взирая на то, что чушь. Единственно, что их частично оправдывает — на 1к реактивная составляющая не так уж и сильно искажает результаты, всего лишь 10-30%, в зависимости от качества аккумулятора (чем лучше, тем больше).
Хотите мерить ESR — используйте ESR-метер.
И R(d.c.) и R(a.c.) — по усмотрению производителя.
Что из этого является бОльшей чушью — лично мне не ведомо.
С большим интересом прочитал.
Тоже часто встречаю на разных ресурсах споры о правильном измерении внутреннего сопротивления ХИТ'ов. Оказывается, всё очень не просто в этом вопросе.
Понравился метод измерения количества теплоты, выделяемой элементом при прохождении калиброванного тока, с последующим пересчетом в эквивалентное сопротивление, на котором выделится такое же количество тепла.
Сама методика замеров жутко сложна и местами стремна. Зависит от ньюансов и требует кучи допущений с неизбежными пересчетами и учетом поправок. И еще неизвестно чего и как им делали (под заказ) ;).
Что я могу сказать — тупо получать R по з-ну Ома для участка цепи и проще и надежнее.
И тоже (по-сути) бессмысленно.
Измерять R гальванического элемента как одиночную величину (типа для куска провода) — затея мягко говоря глупая.
Ибо внутреннее сопротивление гальванического элемента есть сферический конь в вакууме, явного физического смысла не имеет и измерению не подлежит.
Я этот обзор писал для местных электриков (электронщиков, радиолюбителей, «электроников» по диплому из 90-х), но (мне кажется) ни один из электриков этого так и не понял.
На самом деле, к счастью, многие люди (даже достаточно молодые) на просторах экс-СССР до сих пор не превратились в уныло-тупых потребителей бубль-гума. За что им честь и хвала.
Для этого как минимум надо досконально знать и понимать предмет. Удается далеко не всем знающим.
Действительно можно было проще…
Вижу вашу основную мысль, что для аккумуляторов замер R(1кГц) — в основном погода на марсе.
Раз так, то почему бы не взять три кучки аккумов (образцов с одинаковым полезным объемом):
1) токоотдача одинаковая, емкость одинаковая, ресурс разный;
2) ресурс одинаковый, емкость одинаковая, токоотдача разная;
3) ресурс одинаковый, токоотдача одинаковая, емкость разная.
Чем больше вариаций по отличающемуся параметру при двух других равных, тем качественнее будет выборка. Получаем три набора годографов.
На первой кучке выбираем частоту (диапазон) на которой импеданс наиболее характерно показывает разницу в ресурсах аккумов.
На второй кучке выбираем частоту (диапазон) показывающую отличия в токоотдаче.
На третьей, зависимость от емкости.
… Профит!
Если все три полученных диапазона перекрываются, то засекаем частоту наиболее характерно отражающую поведение аккума. Либо просто выбираем по одной характерной точке для каждой кучки, пишем методичку, переводим на китайский, и получаем готовый прибор.
PS. Обзоры читал не по диагонали, но в схемы и формулы не вникал)
Логично выбрать что-то универсальное, постоянное между ними. Такое, что есть у всех.
Самое очевидное — искать на графике какой-то экстремум. Например, справа там провал такой, где Z'' близко к 0, а Z' большое. Либо на «полуокружности» искать локальный максимум, там где -Z'' максимально, а Z' где-то посерединке.
Измерительному прибору тогда делать серию замеров на разных частотах для поиска экстремальных точек.
Несколько выводов или если хотите вопросов:
1. Измерение на 1кГц показывает погоду. Но допустима ли такая погрешность для оценки в практическом применении аккумуляторов, думаю да? (Плохой/хороший или лучше/хуже)
2. Мой пример аналогии с расходом бензина — один прибор, одна реализованная методика измерения разве не позволит узнать отностительную разницу внутренних сопротивлений аккумуляторов с идентичной химией (сравнение одного размера, но разных «производителей» в двух обзорах кирича) почему бы и нет (лучше/хуже во столько то раз)?
Конечно если добавить ячейки с другой химией (к бензиновым двигателям в сравнение паровые или ядерные :-) ) то уже нельзя будет считать даже отностительную разность. В этом вы однозначно правы, исходя из данной статьи.
3. Мне более информативной кажется диаграмма Боде. Как вариант — генератор качающейся частоты пусть будет от 500Гц до 50кГц и поиск минимума комплексного сопротивления и признания его искомым внутренним или, на мой взгляд, ещё более точно измерение этого же комплексного сопротивления в точке сдвига фазы равной нулю. Если мыслю слишком узко, прошу указать почему нельзя так измерять.
4. Совсем непонятно почему LiFePo4 химию так обособили?
— естественного старения самой батареи;
— числа зарядов-разрядов батареи;
— режимов эксплуатации и условий заряда батареи.
Во всех этих процессах меняются свойства электролита, катода и анода, а это ещё больше усложнит понимание внутренних процессов происходящих в ХИТ и изменения внутреннего сопротивления гальванического элемента.
Поэтому ГОСТ поступает мудро — он упрощает ряд процессов, чтобы процесс измерения был доступным, информативным и повторяемым. Не всегда в практическом использовании, а ГОСТ на это и направлен, целесообразно усложнять процесс измерения и получать большое число измеряемых величин.
Автору большое спасибо за его труд. И чтобы его работа не прошла даром ее можно было бы опубликовать в каком то научном журнале, тогда и дискуссия по теме поднятой автором приобрела бы профессиональный характер. Можно было бы и опубликовать и в зарубежном издании и получить грант на дальнейшие изыскания. Желаю автору успехов в дальнейших исследованиях.
Для себя не смог уяснить, при увеличении на сколько процентов внутреннего сопротивления от указанного в даташите аккумулятора мы можем говорить, что сопротивление настолько высокое, что АКБ на утилизацию. Например: в паспорте для нового АКБ 13мОм, а измерили 26мОм то есть увеличение в два раза. Это значит насколько характеристика АКБ ухудшилась? В два раза и в два раза ток он может меньше отдать? Насколько тогда упала ёмкость?
Как такое трактовать, как думаете?
video.aliexpress-media.com/play/u/ae_sg_item/2210511581474/p/1/e/6/t/10301/1100073016374.mp4
mysku.club/blog/diy/94675.html