✧Интегрирование весовым методом. Возрождение забытых технологий
Проверено временем.
Нахождение величины определенного интеграла доступно любому.
Функциональная зависимость y=f(x) — по барабану.
Компьютер не нужен.
Калькулятор — только для ленивых или не умеющих считать без него.
Сейчас в это трудно поверить, но в стародавние времена не было ни интернетов, ни персональных компутеров.
А получать информацию об окружающем мире и проводить научно-технические расчеты хотелось многим. Поэтому древние сапиенсы читали книжки (из бумаги!) и пользовались странными штуковинами для расчетов. Для арифметических расчетов — арифмометрами типа Феликс, для более сложных — логарифмическими линейками и подобными агрегатами.
И именно в те, былинные времена, было придумано интегрирование весовым методом. Скорее всего — химиками. Не потому что они такие умные, а потому что шибко ленивые и хитрые халявщики. А главное — почти поголовно имеющие доступ к одной штуковине по роду своей проф. деятельности. Та девайсина называется «аналитические весы». Это такие весы, которые имеют разрешение по массе навески 0.0001 г. Или чуть больше, вплоть до 0.00001 г. Все, что грубее — это или технические весы или весы для взвешивания колбасы, типа таких
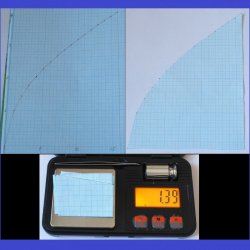
В прошлой жизни аналитические весы выглядели примерно так:
На фото — самая распространенная модель механических аналитических весов АДВ-200. Еще в старинном деревянном корпусе (красное дерево). Потом корпус заменили на металлический — не суть.
Механические аналитические весы — штука капризная, ими нужно было уметь пользоваться и неукоснительно соблюдать кучу нудных правил (полное обучающее видео). Одно неосторожное движение альтернативно одаренного — и грузики («серьги») слетают с положенных мест. Или коромысло слетает с центральной призмы. Поэтому у студентов-химиков регулярно проводился специальный инструктаж. А на младших курсах взвешивание аналитическими весами производилось в присутствии квалифицированного лаборанта в лаборантской.
Понятно, что нонешние электронные модельки на порядки проще в использовании и за каких-то 10-15 минут [в принципе] можно научить любого.
Но и стоят они не кисло. Не, ну на Али можно купить «аналитические» весы значительно дешевле. Но они не будут являться средством измерений.
Да оно нам такое и не нужно.
Суть метода проста. На миллиметровой бумаге рисуется полученная экспериментальная зависимость. Потом все лишнее удаляется ножницами. Площадь под кривой (до оси абсцисс) — есть интеграл по определению. Интеграл находится путем взвешивания вырезанной части бумаги и сравнения с массой прямоугольного куска той же бумаги. Понятно, что чем больше площадь прямоугольника, тем с большей точностью можно определить сколько весит 1 см² миллиметровки.
Но здесь одна закавыка: зависимость показаний весов от измеряемой массы д.б. строго линейной. Изначально это неизвестно. Поэтому весьма желательно сделать какую-никакую калибровку в интересующей нас области значений.
Итак.
Была куплена миллиметровка в листах А4.
Там же прикупил незамысловатые китайские весы с калибровочной гирькой.
Для интересу глянул, что там у нас с миллиметровкой. Оказалось, что все очень даже хорошо. И на 150 мм, и на 50 мм (что в 3 раза менее надежно).
На самом деле, такие красивые погрешности — это нам без разницы. Метод-то сравнительный. И если на бумаге сторона квадратика будет в N раз отличаться от того самого миллиметра, то нам сие несколько по барабану. Главное, что бы N = const по всей плоскости бумаги.
Калибровка
1) Края листов без миллиметровых делений были обрезаны
Потом пошли взвешивания. Каждое взвешивание повторялось 5-6 раз.
2) Было нарезано 5 полос длиной 20 см и шириной 5 см. Оказалось, все они имеют одинаковую массу 0.65 г. Пару раз получилось 0.64 и 0.66 г., но не суть.
3) Масса 5 полос вместе — 500 см².
4) В конце листа еще дополнительные 20х3.5=70 см².
5) Полная масса листа А4 с обрезанными краями
Обратите, внимание — получено 3.76 г., вместо ожидаемых 3.29 (500 см²)+0.48 (70 см²)=3.77 г. Что наглядно демонстрирует недостаток разрядов на малых весах.
6) Путем взвешивания полос 100 см² во всех возможных сочетаниях были получены значения для 200, 300 и 400 см².
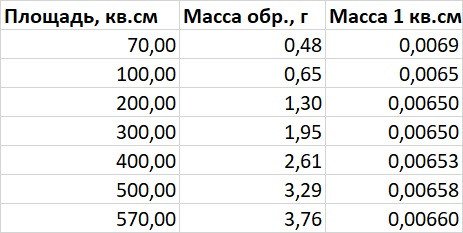
В результате — вот такая табличка:
Важно:
— площадь известна с огромной точностью — до 1 мм².
— а чувствительность определения массы 1 см² лимитируется только чувствительностью весов. До 1 г. имеем всего 2 значащие цифры, а при 1-10 г. — уже 3. Но не стоит обольщаться — в районе 1-2 г. чувствительность больше таковой при 0.8-0.9 г. отнюдь не на порядок.;)
В качестве подопытной была выбрана функция квадратного корня, интеграл которой хорошо известен даже старшеклассникам
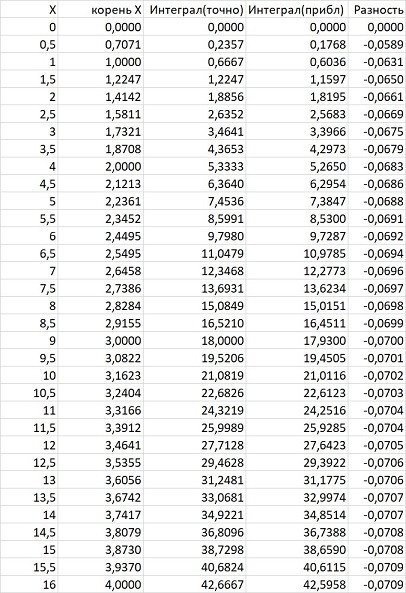
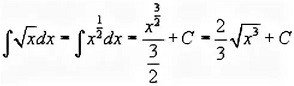В Экселе была получена вот такая табличка
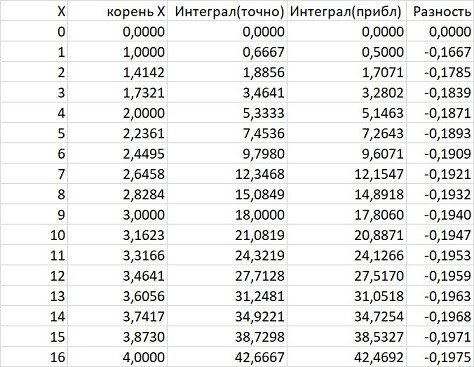Что такое «Интеграл (прибл)» будет объяснено в следующем разделе.
Интегрировать будем в промежутке [0...16].
При симметричных координатах кривая шибко вытянута по оси «Х». Это не есть хорошо.
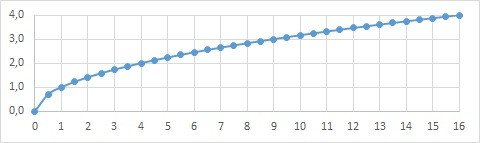В идеале картинка должна быть близка к квадратной. Тогда она наиболее читабельна. Конечно, есть исключения — например, спектры. Но и там их обычно рубят на кусочки и помещают полосами друг под другом.
В данном случае идеальный квадрат получается растягиванием оси «Y» в 4 раза
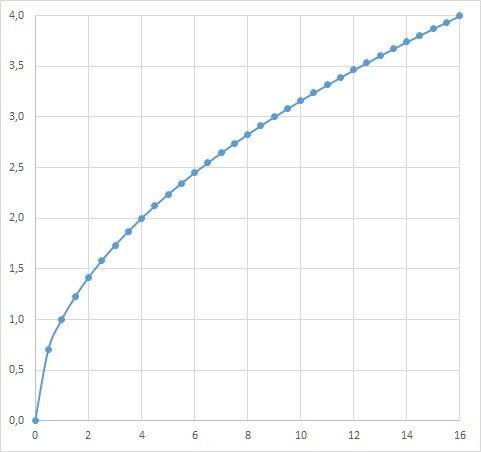Но при построениях на миллиметровке удобнее, если ось растянута не в 4, а в 5 раз.
Есть куда более важный аргумент в пользу растягивания оси «Y» — это вес вырезанной фигуры. Давайте прикинем: если ось «Y» не растягивать, а деления наносить через 1 см, то площадь фигуры будет 42.67 см², а вес — 42.67·0.0065=0.28 г. Это очень мало. Зато после пятикратного растягивания можно получить в районе 42.67·0.0065·5=1.39 г. А это уже более-менее удобоваримо. Тем паче, в калибровочной табличке есть очень близкая реперная точка — это масса 200 см² бумаги.
После взвешивания полученное значение делим на 5 и 0.0065. Это и есть значение интеграла.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Вырезание, складывание в несколько раз и взвешивание:
Собственно, получено то, что и ожидалось — 1.39 г.
Как любил говаривать один известный (в прошлом) фокусник Акопян «Ловкость рук, и никакого мошенства». На самом деле, сей фразеологический оборот был просто позаимствовал.
Но не спешите радоваться — интеграл найден не так что бы уж сильно точно и неминуемо набежало 0.1 абсолютной погрешности, а это ~2.3 % относительной.
1.39/(5·0.00650)=42.7692...=42.8 — увы, три значащие циферки в лучшем случае.
А должно быть 42.6667=42.7.
В принципе, такая погрешность при проведении экспериментальных исследований не так уж и плоха. Прямые и косвенные замеры измеряемой величины с относительной погрешностью 5-7% раньше считались количественными. Как оно сейчас — не интересовался.
Можно ли попробовать увеличить чувствительность? Теоретически — да. На вскидку, могу сразу предложить целых три «путЯ».
Вариант №1 (для ленивых)
Купить технические весы 0.001 г. и калибровочные гирьки к ним.
Тем паче, у китайцев такое можно найти за недорого, те же 1-2 тыс. руб. Одно плохо — счастливые обладатели оных постоянно жалуются, что 3 знак после запятой — скорее всего фикция. Типа как куча лишних разрядов в нонешних USB-докторах;)
А приличные высокоточные технические весы от аналитических по цене не сильно отличаются. И по капризности при использовании — тоже. Ибо суть и внутренний мир практически одинаковы.
Вариант №2 (для неленивых)
Вырезать 10 таких фигур (той же площади) и взвесить их скопом.
Вариант №3 (для неленивых)
Посчитать квадратики на миллиметровке
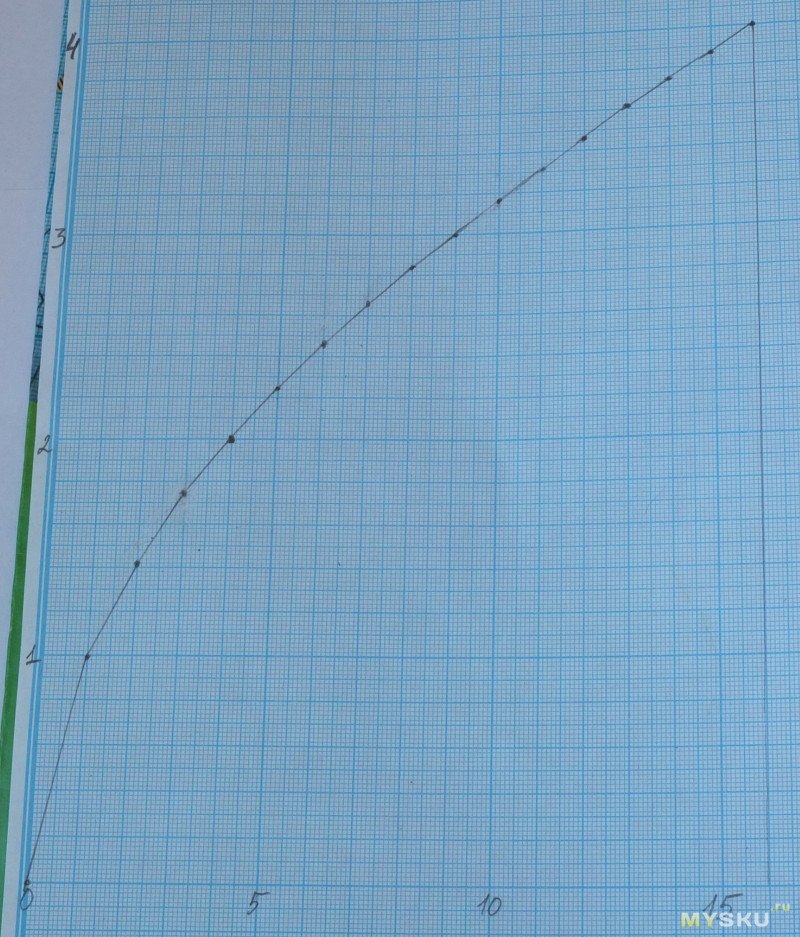
Помните известную притчу о количестве дырочек в барабане стиральной машины?;)
На самом деле, посчитать площадь фигуры не так уж и сложно, если разбивать на полигоны. Сначала большие, потом меньше и меньше. А полученную сумму не забыть поделить на 5. Наверное, это будет наиболее точное определение площади данного построения. И весы не нужны.***
***Прим. На самом деле — в прошлой жизни для переноса площади под кривой или относительно широких пиков со спектрофотограмм, рентгенограмм, хроматограмм и т.п. чаще использовалась не столько миллиметровка, сколько полупрозрачная бумага типа кальки. Интеграл дает количественную оценку содержания компонента в анализируемом объекте/смеси веществ.
Ибо тут собака порылась еще и в другом. Причем, основательно. Это не значит, что предложенные варианты изначально бессмысленны. Просто для конкретно данного примера они не приведут к какому-либо улучшайтингу.
Вернемся к нашим баранам — что такое «Интеграл (прибл)» в табличке выше?
А это интеграл, вычисленный методом средних прямоугольников, наиболее простым и популярным способом нахождения интегралов на основании экспериментальных данных. Есть еще методы левых и правых прямоугольников, для тех, кто «знал, но забыл» можно глянуть здесь. При одном и том же количестве разбиений (экспериментальных точек), метод средних прямоугольников дает значение определённого интеграла более близкое у «истинному». И чем меньше тех точек — тем сильнее это чувствуется.
Посмотрите на крайнюю правую колонку в рассматриваемой табличке — это абсолютная погрешность нахождения интеграла методом средних прямоугольников относительно точного значения. Нетрудно заметить, что львиная доля (84.4%) той погрешности приходится на 1-ое измерение.
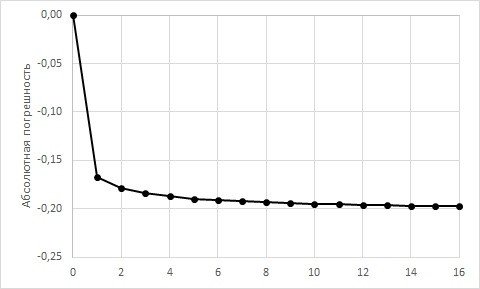
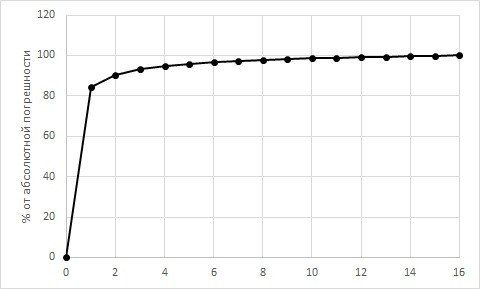Можно ли уменьшить ту погрешность? Легко. Просто увеличить частоту разбиения.
Но проблема в том, что без автоматической записи такое часто невозможно. Плюс неизбежные экспериментальные погрешности измерений.
Пример взят отсюда. Это опыт №2, кривая разряда Epilso LR44 до 1.2 В:
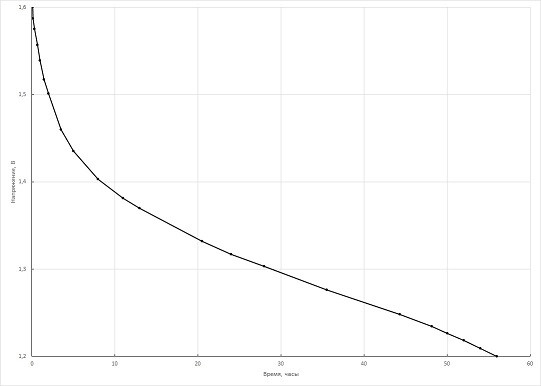Расчет по формуле:
Емкость = I·t = (U/R)·t
R = Rн + r = Rн, так как Rн (нагрузка) >>r (т.н. «внутреннее сопротивление»)
Rн = 676 Ω для данной кривой. А r ориентировочно на два порядка меньше. Точнее сказать не могу, но я провел дополнительный эксперимент с 4 экз. LR44 Epilso по дробному разряду (по 9-10 час) с замерами импеданса на 1кГц в промежутках. Вплоть до 0.9 В (под нагрузкой) импеданс меняется слабо и составляет ~2.5-3.5 Ω. Когда-нибудь опубликую краткий отчет.
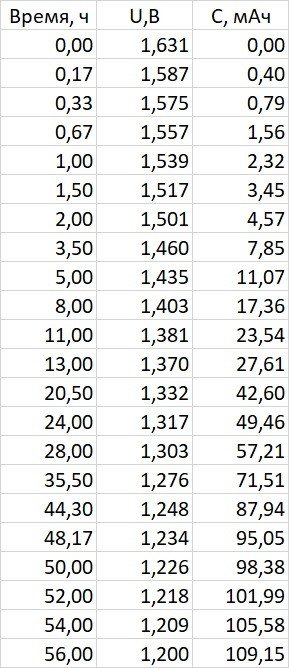
В итоге 109.15 мАч. Если округлить до 3 значащих, то 109 мАч.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Теперь попробуем определить емкость с помощью бумаги.
Итак, масса вырезанной фигуры 1.06 г. Дальше все очень просто [для левополушарных].
1) Ось «Х» («часы») сжата в 2 раза. А ось «Y» («вольты») растянута в 50 раз. Значит, полученное значение нужно поделить на К=50/2=25. И еще поделить на 0.00650 г/см²
U·t=1.06/(25·0.00650).
2) Перевести в амперы (поделить на R), перевести в миллиамперы (умножить на 1000)
I·t=U·t/R=1000·(1.06/25·0.00650)/676=1060/(25·0.00650·676)=9.64952...=9.65 мАч
Но это не полная емкость, а «емкость» вырезанной части.
Емкость = 9.65 мАч + С
3) «Интегрирование» начиналось не от нуля, от 1.2В. Свободный член «С» — пропорционален площади прямоугольника со сторонами, соответствующими 56 ч. и 1.2В. Это 28·60=1680 см². Что соответствует массе 1680(см²)·0.00650(г/см²)=10.92 г.
С = 1000·(10.92/25·0.00650)/676 = 10920/(25·0.00650·676) = 99.4082… = 99.41 мАч
4) Емкость = 9.65 + 99.41 = 109.06 мАч. Великолепное совпадение с «компутерными» 109.15 мАч. Но округлять придется до 3 значащих циферок, т.к. масса «выкройки» известна только с 3 значащими и величина 0.00650 г/см² — это тоже всего 3 значащих. Так что окончательно — только 109 мАч без запятой.
Увы, но так надо, товарищ.
Я специально сделал кучу лишних действий. Исключительно ради понимания незамысловатой логики расчётов. Спасибо тем, кто смог осилить до этого места.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
На этом все. Желаю всем удачных взвешиваний интегралов с минимальными погрешностями.
Всего доброго.
Нахождение величины определенного интеграла доступно любому.
Функциональная зависимость y=f(x) — по барабану.
Компьютер не нужен.
Калькулятор — только для ленивых или не умеющих считать без него.
Преамбула
Сейчас в это трудно поверить, но в стародавние времена не было ни интернетов, ни персональных компутеров.
А получать информацию об окружающем мире и проводить научно-технические расчеты хотелось многим. Поэтому древние сапиенсы читали книжки (из бумаги!) и пользовались странными штуковинами для расчетов. Для арифметических расчетов — арифмометрами типа Феликс, для более сложных — логарифмическими линейками и подобными агрегатами.
Дополнительная информация. Содержит контент 16+!
Советские логарифмические линейки от забугорных прародителей отличались наличием на одном из торцов обычной сантиметрово-миллиметровой шкалы, что позволяло использовать логарифмическую линейку как обычную линейку. В 70-х правила пользования логарифмическими линейками изучались уже в старших классах общеобразовательных школ.
И тогда был рожден классический анекдот:
И тогда был рожден классический анекдот:
Едет троллейбус. Вдруг троллейбус резко тормозит и юная дама непроизвольно приземляется на колени сидящего рядом молодого человека:
— Ого! — вскрикивает она.
— Да не «ого», а логарифмическая линейка. — резонно замечает мол.чел.
И именно в те, былинные времена, было придумано интегрирование весовым методом. Скорее всего — химиками. Не потому что они такие умные, а потому что шибко ленивые и хитрые халявщики. А главное — почти поголовно имеющие доступ к одной штуковине по роду своей проф. деятельности. Та девайсина называется «аналитические весы». Это такие весы, которые имеют разрешение по массе навески 0.0001 г. Или чуть больше, вплоть до 0.00001 г. Все, что грубее — это или технические весы или весы для взвешивания колбасы, типа таких
В прошлой жизни аналитические весы выглядели примерно так:На фото — самая распространенная модель механических аналитических весов АДВ-200. Еще в старинном деревянном корпусе (красное дерево). Потом корпус заменили на металлический — не суть.Механические аналитические весы — штука капризная, ими нужно было уметь пользоваться и неукоснительно соблюдать кучу нудных правил (полное обучающее видео). Одно неосторожное движение альтернативно одаренного — и грузики («серьги») слетают с положенных мест. Или коромысло слетает с центральной призмы. Поэтому у студентов-химиков регулярно проводился специальный инструктаж. А на младших курсах взвешивание аналитическими весами производилось в присутствии квалифицированного лаборанта в лаборантской.
Понятно, что нонешние электронные модельки на порядки проще в использовании и за каких-то 10-15 минут [в принципе] можно научить любого.
Картинки
Но и стоят они не кисло. Не, ну на Али можно купить «аналитические» весы значительно дешевле. Но они не будут являться средством измерений.
Да оно нам такое и не нужно.
В статье будет рассмотрена возможность применения недорогих китайских «ювелирных» весов с разрешением 0.01 г.
Суть метода и калибровка
Суть метода проста. На миллиметровой бумаге рисуется полученная экспериментальная зависимость. Потом все лишнее удаляется ножницами. Площадь под кривой (до оси абсцисс) — есть интеграл по определению. Интеграл находится путем взвешивания вырезанной части бумаги и сравнения с массой прямоугольного куска той же бумаги. Понятно, что чем больше площадь прямоугольника, тем с большей точностью можно определить сколько весит 1 см² миллиметровки.
Но здесь одна закавыка: зависимость показаний весов от измеряемой массы д.б. строго линейной. Изначально это неизвестно. Поэтому весьма желательно сделать какую-никакую калибровку в интересующей нас области значений.
Итак.
Была куплена миллиметровка в листах А4.
Там же прикупил незамысловатые китайские весы с калибровочной гирькой.Для интересу глянул, что там у нас с миллиметровкой. Оказалось, что все очень даже хорошо. И на 150 мм, и на 50 мм (что в 3 раза менее надежно).На самом деле, такие красивые погрешности — это нам без разницы. Метод-то сравнительный. И если на бумаге сторона квадратика будет в N раз отличаться от того самого миллиметра, то нам сие несколько по барабану. Главное, что бы N = const по всей плоскости бумаги.Калибровка
1) Края листов без миллиметровых делений были обрезаны
Потом пошли взвешивания. Каждое взвешивание повторялось 5-6 раз.
2) Было нарезано 5 полос длиной 20 см и шириной 5 см. Оказалось, все они имеют одинаковую массу 0.65 г. Пару раз получилось 0.64 и 0.66 г., но не суть.
3) Масса 5 полос вместе — 500 см².
4) В конце листа еще дополнительные 20х3.5=70 см².
5) Полная масса листа А4 с обрезанными краями
Обратите, внимание — получено 3.76 г., вместо ожидаемых 3.29 (500 см²)+0.48 (70 см²)=3.77 г. Что наглядно демонстрирует недостаток разрядов на малых весах.6) Путем взвешивания полос 100 см² во всех возможных сочетаниях были получены значения для 200, 300 и 400 см².
В результате — вот такая табличка:
Важно:— площадь известна с огромной точностью — до 1 мм².
— а чувствительность определения массы 1 см² лимитируется только чувствительностью весов. До 1 г. имеем всего 2 значащие цифры, а при 1-10 г. — уже 3. Но не стоит обольщаться — в районе 1-2 г. чувствительность больше таковой при 0.8-0.9 г. отнюдь не на порядок.;)
Проверка метода на известном значении интеграла
В качестве подопытной была выбрана функция квадратного корня, интеграл которой хорошо известен даже старшеклассникам
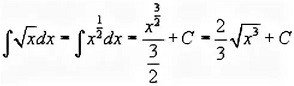В Экселе была получена вот такая табличкаЧто такое «Интеграл (прибл)» будет объяснено в следующем разделе.Интегрировать будем в промежутке [0...16].
При симметричных координатах кривая шибко вытянута по оси «Х». Это не есть хорошо.
В идеале картинка должна быть близка к квадратной. Тогда она наиболее читабельна. Конечно, есть исключения — например, спектры. Но и там их обычно рубят на кусочки и помещают полосами друг под другом.В данном случае идеальный квадрат получается растягиванием оси «Y» в 4 раза
Но при построениях на миллиметровке удобнее, если ось растянута не в 4, а в 5 раз.Есть куда более важный аргумент в пользу растягивания оси «Y» — это вес вырезанной фигуры. Давайте прикинем: если ось «Y» не растягивать, а деления наносить через 1 см, то площадь фигуры будет 42.67 см², а вес — 42.67·0.0065=0.28 г. Это очень мало. Зато после пятикратного растягивания можно получить в районе 42.67·0.0065·5=1.39 г. А это уже более-менее удобоваримо. Тем паче, в калибровочной табличке есть очень близкая реперная точка — это масса 200 см² бумаги.
После взвешивания полученное значение делим на 5 и 0.0065. Это и есть значение интеграла.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Вырезание, складывание в несколько раз и взвешивание:
Собственно, получено то, что и ожидалось — 1.39 г.Как любил говаривать один известный (в прошлом) фокусник Акопян «Ловкость рук, и никакого мошенства». На самом деле, сей фразеологический оборот был просто позаимствовал.
Но не спешите радоваться — интеграл найден не так что бы уж сильно точно и неминуемо набежало 0.1 абсолютной погрешности, а это ~2.3 % относительной.
1.39/(5·0.00650)=42.7692...=42.8 — увы, три значащие циферки в лучшем случае.
А должно быть 42.6667=42.7.
В принципе, такая погрешность при проведении экспериментальных исследований не так уж и плоха. Прямые и косвенные замеры измеряемой величины с относительной погрешностью 5-7% раньше считались количественными. Как оно сейчас — не интересовался.
Можно ли попробовать увеличить чувствительность? Теоретически — да. На вскидку, могу сразу предложить целых три «путЯ».
Вариант №1 (для ленивых)
Купить технические весы 0.001 г. и калибровочные гирьки к ним.
Тем паче, у китайцев такое можно найти за недорого, те же 1-2 тыс. руб. Одно плохо — счастливые обладатели оных постоянно жалуются, что 3 знак после запятой — скорее всего фикция. Типа как куча лишних разрядов в нонешних USB-докторах;)
А приличные высокоточные технические весы от аналитических по цене не сильно отличаются. И по капризности при использовании — тоже. Ибо суть и внутренний мир практически одинаковы. Вариант №2 (для неленивых)
Вырезать 10 таких фигур (той же площади) и взвесить их скопом.
Вариант №3 (для неленивых)
Посчитать квадратики на миллиметровке
Полноразмеры для желающих
Помните известную притчу о количестве дырочек в барабане стиральной машины?;)
На самом деле, посчитать площадь фигуры не так уж и сложно, если разбивать на полигоны. Сначала большие, потом меньше и меньше. А полученную сумму не забыть поделить на 5. Наверное, это будет наиболее точное определение площади данного построения. И весы не нужны.***
***Прим. На самом деле — в прошлой жизни для переноса площади под кривой или относительно широких пиков со спектрофотограмм, рентгенограмм, хроматограмм и т.п. чаще использовалась не столько миллиметровка, сколько полупрозрачная бумага типа кальки. Интеграл дает количественную оценку содержания компонента в анализируемом объекте/смеси веществ.
Ибо тут собака порылась еще и в другом. Причем, основательно. Это не значит, что предложенные варианты изначально бессмысленны. Просто для конкретно данного примера они не приведут к какому-либо улучшайтингу.Метод средних прямоугольников. И почему увеличение «чувствительности» в данном случае — дорога в никуда
Вернемся к нашим баранам — что такое «Интеграл (прибл)» в табличке выше?
А это интеграл, вычисленный методом средних прямоугольников, наиболее простым и популярным способом нахождения интегралов на основании экспериментальных данных. Есть еще методы левых и правых прямоугольников, для тех, кто «знал, но забыл» можно глянуть здесь. При одном и том же количестве разбиений (экспериментальных точек), метод средних прямоугольников дает значение определённого интеграла более близкое у «истинному». И чем меньше тех точек — тем сильнее это чувствуется.
Посмотрите на крайнюю правую колонку в рассматриваемой табличке — это абсолютная погрешность нахождения интеграла методом средних прямоугольников относительно точного значения. Нетрудно заметить, что львиная доля (84.4%) той погрешности приходится на 1-ое измерение.
Можно ли уменьшить ту погрешность? Легко. Просто увеличить частоту разбиения. В 2 раза чаще - в 3 раза меньше погрешность
Но проблема в том, что без автоматической записи такое часто невозможно. Плюс неизбежные экспериментальные погрешности измерений.
Метод средних прямоугольников VS взвешивание бумаги на примере измерения емкости батарейки самым простым способом
Пример взят отсюда. Это опыт №2, кривая разряда Epilso LR44 до 1.2 В:
Расчет по формуле: Емкость = I·t = (U/R)·t
R = Rн + r = Rн, так как Rн (нагрузка) >>r (т.н. «внутреннее сопротивление»)
Rн = 676 Ω для данной кривой. А r ориентировочно на два порядка меньше. Точнее сказать не могу, но я провел дополнительный эксперимент с 4 экз. LR44 Epilso по дробному разряду (по 9-10 час) с замерами импеданса на 1кГц в промежутках. Вплоть до 0.9 В (под нагрузкой) импеданс меняется слабо и составляет ~2.5-3.5 Ω. Когда-нибудь опубликую краткий отчет.
Экспериментальные точки и расчет емкости
В итоге 109.15 мАч. Если округлить до 3 значащих, то 109 мАч.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Теперь попробуем определить емкость с помощью бумаги.
Выкройка
Это полноразмеры. Для желающих посчитать клеточки.:)
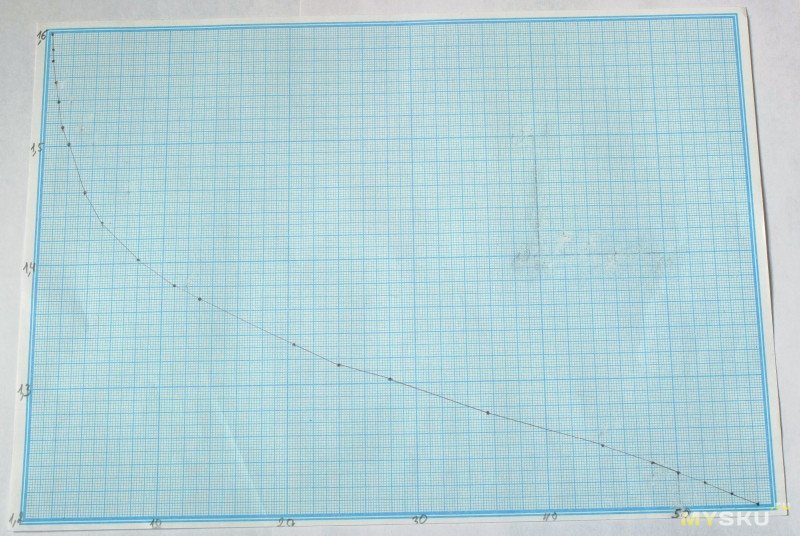
Итак, масса вырезанной фигуры 1.06 г. Дальше все очень просто [для левополушарных].
1) Ось «Х» («часы») сжата в 2 раза. А ось «Y» («вольты») растянута в 50 раз. Значит, полученное значение нужно поделить на К=50/2=25. И еще поделить на 0.00650 г/см²
U·t=1.06/(25·0.00650).
2) Перевести в амперы (поделить на R), перевести в миллиамперы (умножить на 1000)
I·t=U·t/R=1000·(1.06/25·0.00650)/676=1060/(25·0.00650·676)=9.64952...=9.65 мАч
Но это не полная емкость, а «емкость» вырезанной части.
Емкость = 9.65 мАч + С
3) «Интегрирование» начиналось не от нуля, от 1.2В. Свободный член «С» — пропорционален площади прямоугольника со сторонами, соответствующими 56 ч. и 1.2В. Это 28·60=1680 см². Что соответствует массе 1680(см²)·0.00650(г/см²)=10.92 г.
С = 1000·(10.92/25·0.00650)/676 = 10920/(25·0.00650·676) = 99.4082… = 99.41 мАч
4) Емкость = 9.65 + 99.41 = 109.06 мАч. Великолепное совпадение с «компутерными» 109.15 мАч. Но округлять придется до 3 значащих циферок, т.к. масса «выкройки» известна только с 3 значащими и величина 0.00650 г/см² — это тоже всего 3 значащих. Так что окончательно — только 109 мАч без запятой.
Увы, но так надо, товарищ.
Я специально сделал кучу лишних действий. Исключительно ради понимания незамысловатой логики расчётов. Спасибо тем, кто смог осилить до этого места.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
На этом все. Желаю всем удачных взвешиваний интегралов с минимальными погрешностями.
Всего доброго.
Самые обсуждаемые обзоры
| +71 |
3366
134
|
| +51 |
3572
66
|
| +29 |
2535
48
|
| +38 |
2894
41
|
| +55 |
2043
37
|
:)))
Едет троллейбус. Вдруг троллейбус резко тормозит и девушка непроизвольно приземляется на колени сидящего священика:
— Ого-го! — вскрикивает она.
— То не «ого-го», то ключ от церкви. — уточняет священник.
Ведь что такое анекдот!? Короткий забавный случай из жизни.
Аналоговый вычислитель, ценность, это ж целая отрасль была.
ножнахчехле на поясе, обычно сбоку. Сидеть так, чтобы ого-го, и самому неудобно будет, и ценный инструмент портится.Разные бывают линейки…
Замечу что дико неудобно жить без черты площади круга. А линза хоть и даёт мелкой линейке какое-то подобие точности, но полностью исключает нецентральные черты.
И решать ничего не надо — это стандартный «табличный» интеграл.
ТАБЛИЦА ИНТЕГРАЛОВ
«горидовка» — ?
А уж интеграл степенной ф-ии — это 5 сек поиска в Гугле-Яндексе:
А когда то искалось не в гугле, а в голове, причем моментально.
Вы — один из немногих, кого спрашивал, и кому вся эта вышка потом по жизни пригождалась. Не считая, понятно, тех, кто работает по профилю.
И больше всего из вышки мне пригодилось умение учиться…
— «вышка» — это есть ВУЗ, в коем Вы учились или
— раздел математики, который даже на самом элементарном уровне (тупо — бесконечно малые приращения) уже принято относить к «высшей»?
Хотя, в общем то, обе пригодились.
А высшая математика в жизни нафиг не пригождается, если не по работе только.
А вот сын его Иван Дмитриевич постарался
ссылка
Получается, сына Менделеева в честь деда назвали )
позанудствую
1. В этих весах погрешность еще зависит от того, где именно находится груз. Причем, допустим, нижний правый край <> левому краю (на моих так)
2. Я правильно понимаю, что в самих весах есть много точек калибровки и там соответствие сигнала с датчика к весу груза может быть сильно нелинейно?
Подробности ТУТ, начиная с 3:35.
Это на Ваших так...;)
Насчет «сильно» — это вряд ли. А вот насчет некоторой слабой нелинейности на малых весах моего экземпляра — я продемонстрировал в табличке. БОльшие веса не проверял — пока нет такой необходимости.)
Вот тут на фотке. mysku.club/blog/aliexpress/28053.html
это сильно увеличит разрядность, так как такие весы вроде бы килограм измеряют
Но у меня есть сильное прозрение, что это есть «разогнанный» вариант 0-100 г.
Причин две, но это долго, нудно и пока из области предположений.)
А то у меня флешбек дипломной работы про мат моделирование вакуумных систем.
И сгенерёные в экселе двумерные карты распределения давления, напечатанные на цветном принтере, висевшие чуть не 10 лет на кафедре за спиной у дипломного руководителя. До сих пор помню, как ему приятно было, когда был виден «сток» молекул рядом с местом подключения вакуумного насоса. Очень ему тогда всё это понравилось :)
Предлагали записываться в очередь в ВЦ института, но мне было лень.
Уравнение я решил, уже не помню, каким методом — я их кучу перепробовал.
Но что меня тогда несколько удивило — самая быстрая сходимость была именно у метода Монте-Карло.
По крайней мере на том уравнении, что мне прищлось решать…
Тогда будем оперировать уже десятой частью грамма,
Берется станок плазменной резки, само собой — с ЧПУ, х сейчас и нет других.
Берется лист стали десятки, в станок загоняется формула, результат отвозится на автомобильные весы…
(Работаю на металлобазе и в круг моих обязанностей входит учёт)
С — произвольная постоянная, которая включается в выражение для неопределённого интеграла, так как производная от константы равна нулю.
При вычислении определённого интеграла её быть не может, вычтется она сама из себя :). Откуда бы кривая ни выходила :).
Если эта кривая выходит из начала координат, то свободный член С=0
А в чем ее смысл?
Для простоты рассуждений ограничимся 1-ым квадрантом координатной плоскости и интегрированием от 0 вправо.
Неопределенный интеграл задает семейство первообразных, отличающихся только на С, где С = [-∞,+∞].
По сути, величина С определяется длинами отрезков А и В
С=А·В.
где А — отрезок по «X» (на котором берется определенный интеграл)
В — отрезок по «Y» — есть расстояние от начала координат до места пересечения с «Y» (ибо интегрируем от 0!). Вот и все рассуждения, изложенные в статье. Наверное, зря я это Вам рассказываю — скорее всего Вы это итак понимаете…
Если бы взятая вами функция на выходила из начала координат (например, f(x)=√x +5), то неопределенный интеграл был бы уже другой, но в его выражении все равно присутствовало бы неизвестное С
Все верно. Это бесконечное множество интегрируемых кривых, которое сдвигается вверх-вниз на величину Z = [-∞,+∞]. Из-за этого и появляется в интеграле С = [-∞,+∞].)
С в интеграле появляется по определению этого самого интеграла, так как производная от константы равна нулю :). При сдвигании подынтегральной функции f(x) вверх-вниз меняется первообразная функция F(x), как я показал вам в рукописном примере в сообщении выше. Там добавился еще один член в выражении, 5х. Как раз в результате сдвига f(x) на 5 единиц вверх.
К счастью, при вычислении определенного интеграла на участке [a;b] по формуле Ньютона-Лейбница знать значение С не требуется, так как (F(b) + C) — (F(a) + C) = F(b) — F(a). С просто сокращается, чему бы оно ни было равно. Поэтому о нем можно просто «забыть», но говорить, что оно равно нулю не верно.
А главное, что дошло: между неопр. и опр. интегралами — пропасть. Это как теплое и мягкое.
Неопр. и. — это ф-ия, да еще содержащая вечно неизвестную «С». Нужна исключительно для нахождения опр.и. А опр. и. — это уже число.
Спасибо за полезное обсуждение.
ЗЫ. Лишнее предложение убрал в статье.
Зачастую важно знать именно функциональную зависимость. Самый простой пример из школьной физики — равноускоренное движение. Зависимость ускорения от времени а(t)=a. Скорость — это интеграл от ускорения по времени. Взяв его, получаем формулу v(t)=a*t + C1. В данном случае С1 имеет смысл скорости в момент времени t=0, то есть начальной. И мы сразу получаем то, что помним со школы v(t) = v0 + a*t. Проинтегрировав скорость по времени, получим формулу для пути s(t) = v0*t + a*t²/2 + C2. И опять С2 имеет вполне определенный смысл — путь, пройденный телом в момент времени t=0.
ЗЫ. Посмотрел список Ваших статей. Оказалось, с большей частью знаком.)
Завидую белой завистью энтузиазму и количеству свободного времени автора!
Но… пусть лучше так маньячить, чем на улицах, например)
Жир с пальцев чувствуется только 4-ом знаке после запятой.
Поэтому все операции с разновесами на аналит. весах — только чистым пинцетом…
Просто увидел только сейчас .